1. Properties of parallel lines

                                         

 
One of the signs of parallel lines on a plane is:

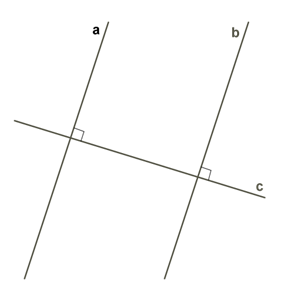
This feature is easy to prove if we recall that only one perpendicular can be drawn to a line in a plane from any point.
 
Suppose, the lines perpendicular to the same line are not parallel, that is, they have a common point.
 

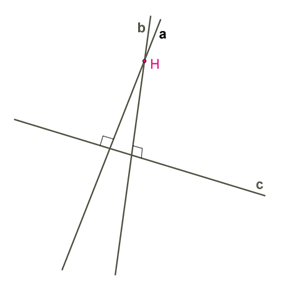
It turns out a contradiction - point \(H\) is straight to point \(c\), two perpendiculars are seen. It is impossible, therefore two lines on the plane, perpendicular to the same line, are parallel.
 

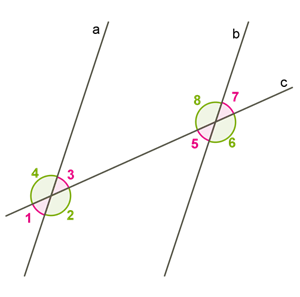
1) Names and properties of the angles that form two intersecting straight lines are:

 
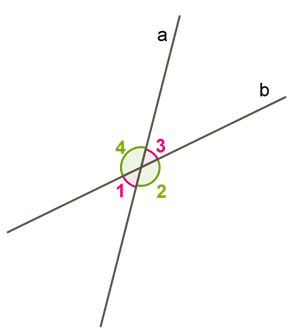
The vertical angles are $\measuredangle 1=\measuredangle 3;\measuredangle 2=\measuredangle 4$.
Sum of adjacent corners will be $180°$: $\measuredangle 1+\measuredangle 2=\measuredangle 2+\measuredangle 3=\measuredangle 3+\measuredangle 4=\measuredangle 4+\measuredangle 1=180°$.

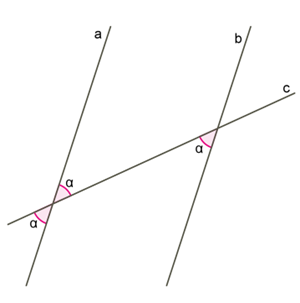
2) If two lines intersect the third line, then the angles are called like this:

 

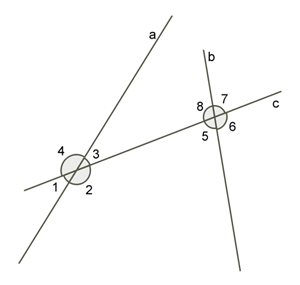
lying corners: $\measuredangle 3$ and $\measuredangle 5$; $\measuredangle 2$ and $\measuredangle 8$;
corresponding angles: $\measuredangle 1$ and $\measuredangle 5$; $\measuredangle 4$ and $\measuredangle 8$; $\measuredangle 2$ and $\measuredangle 6$; $\measuredangle 3$ and $\measuredangle 7$;
one-sided angles: $\measuredangle 3$ and $\measuredangle 8$; $\measuredangle 2$ and $\measuredangle 5$.

These angles will help determine the parallelism of the lines \(a\) and \(b\). So, another sign of parallelism of lines on the plane is: 

 
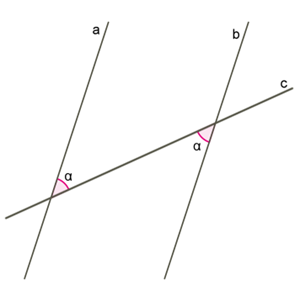
Let us prove this feature.
 
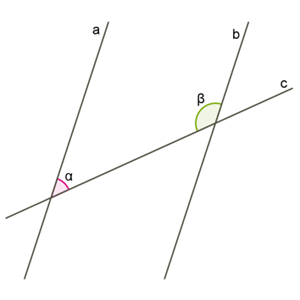
If the lines \(a\) and \(b\) cross a straight line \(c\), and the angles lying are equal, then the straight lines \(a\) and \(b\) are parallel.
 
For example, if $\measuredangle 3=\measuredangle 5$ then $a\parallel b$.
  
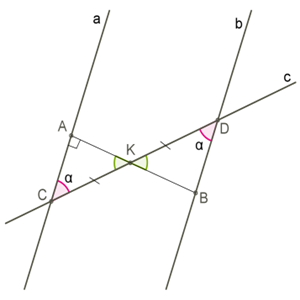
1) Note the points \(C\)  and \(D.\) In which direct \(a \) and \(b \) crosses a straight line \(c\). Through, the midpoint \(K\) draw a perpendicular of this segment \(AB\) to straight \(a\).
2) $\measuredangle \mathit{CKA}=\measuredangle \mathit{DKB}$ like vertical angles $\measuredangle 3=\measuredangle 5=\mathrm{\alpha }$, \(CK=KD\) which means $\mathrm{\Delta }\mathit{CKA}=\mathrm{\Delta }\mathit{DKB}$ based on a side and two adjacent corners.
3) If $\mathrm{\Delta }\mathit{CKA}$ and $\mathrm{\Delta }\mathit{DKB}$ are equal, then AB is perpendicular to straight b.
4) According to the first proven feature, the lines perpendicular to the same line are parallel.
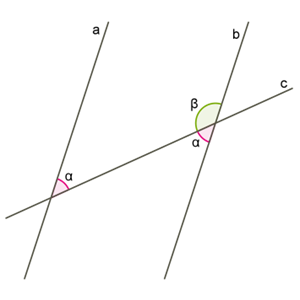
5) In the case when the corresponding angles are equal, we mean that the vertical angles are equal, and we prove, as in paragraphs 1) - 4).
  
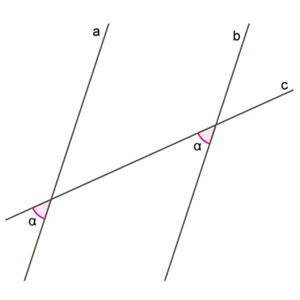
6) In the case when the sum of one-sided angles is $180°$, we mean that the sum of adjacent angles is also equal $180°$, and we use paragraphs 1) - 4) in the proof. 
  
3. The sign of parallel lines also acts as a property of parallel lines.