UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreA closed line consisting of all points on the plane that are equidistant from a given point on the plane is called a circle.
- In the definition, the given point on the plane is called the center of the circle. Usually, we denote the center by the letter O.
- The circle is called the circle along with the part of the plane it delimits.
To draw a circle, take a compass with a pen/pencil attached to it and place the sharp end of the compass on a particular point of a paper, then keeping the abrupt end non-movable rotate the compass 360 degrees, so the pen/pencil draws a perfect circle.
The circle, in the drawing, is black. The black line, together with the shaded area forms a circle. Where, O is the center of the circle.
- The segment joining the center to a freely chosen point on the circumference is called the radius. We usually denote radius by the lowercase r or the uppercase R.
- The segment that joins the two points of the circle is called a chord.
- The chord passing through the center of the circle is called the diameter.
or , where d is the diameter of the circle and R is the radius of the circle.
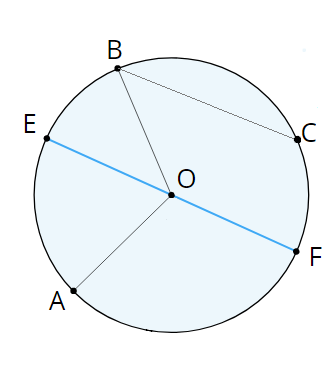
AO=BO=EO=FO as circular radii.
The radii EO and FO form the diameter EF.
BC is a chord.
Register for free to see more content