UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreFamiliarize yourself with the mathematics tool - the Compass.
Compass can look different, but all whips have two legs - a sharp-pointed pin and a pencil.
Compass can be used to draw a circle.
If you mark a small mark or dot on a piece of paper and place the sharp crank leg at that point, you can draw a circle. The dot is called the center of the circle, and we usually denote by the capital letter O.
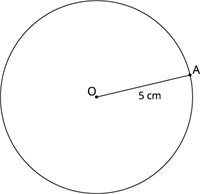
The segment joining center O of a circle to a point on the circle (point A in the drawing) is called the radius.
The figure shows that the radius of the circle OA is 5cm (Figure: 1).
Compass is needed - with the feet of the cruiser measured to the desired distance to draw a circle with a given radius.
Figure: 1
- The coloured part inside is the area of a circle. (Figure: 2).
Figure: 2
The segment passing through the center of the circle and joining the two points of the circumference is called the diameter.
- The diameter is EF (Figure: 3).
Figure: 3
- The segments AO, BO, CO, EO, FO are the radii of the circumference (Figure: 3).
The radii of the circle are equal in length.
AO = BO = CO = EO = FO
AO = BO = CO = EO = FO
The diameter of the circle is 2 times longer than the radius.
If the radius of the circle is 5cm, then the diameter is 2·5 = 10 (cm).
Register for free to see more content