PDF chapter test TRY NOW
An exterior angle of a triangle is equal to the sum of its opposite interior angles.
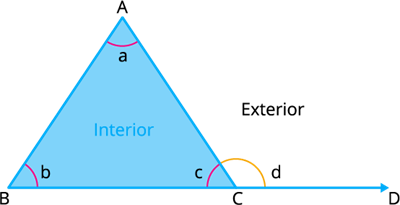
For vertex \(C\), the interior angle is \(∠ACB = c\) and the exterior angle is \(∠ACD = d\).
By the property, we can write that:
\(∠ACD = ∠CAB + ∠CBA\).
That is, \(d = a+b\).
Let's prove this statement through logical argument.
An exterior angle of a triangle is equal to the sum of its interior opposite angles.
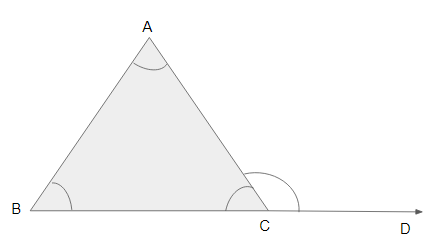
Given:
Consider a triangle \(ABC\) with extended line \(CD\) forms an exterior angle to vertex \(C\).
To prove:
\(∠ACD = ∠A + ∠B\).
We will prove this using alternate angles property.
Let's draw a line \(CE\) from \(C\) which is parallel to \(AB\).
Take the line \(AC\) as transversal.
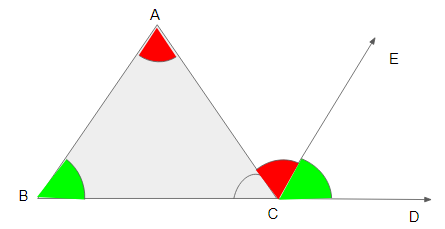
By alternate interior angle property, \(∠A = ∠ACD\) [alternate interior angles are equal in measure].
Now take the line \(BD\) as transversal for the parallel lines \(AB\) and \(CD\).
By corresponding angles property,\(∠B = ∠ECD\) [corresponding angles are equal in measure].
\(∠ACD = ∠ACE + ∠ECD = ∠A + ∠B\)
Thus, it is obvious that the exterior angle of a triangle is equal to the sum of its opposite interior angles.
Register for free to see more content