UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreThe inverse operation of a cube is cube root. The symbol used to represent the cube root is \(\sqrt[3]{}\).
A cube root is a unique value that gives us the original number when we multiply itself by three times.
The cube root of \(a\) is denoted by \(\sqrt[3]{a}\) or \(a^{\frac{1}{3}}\).
Example:
Find the cube root of \(64\).
Solution:
\(\sqrt[3]{64} = \sqrt[3]{4 \times 4 \times 4}\) \(= \sqrt[3]{4^3}\) \( = 4\)
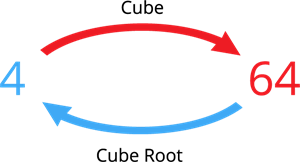
Therefore, the cube root of \(64\) is \(4\).
By the observation of the above example, we can conclude that:
The cube of \(4\) is \(64\).
The cube root of \(64\) is \(4\).
The following table consist of cube and cube roots of the first \(20\) numbers.
Number | Cube number | Cube root | Number | Cube number | Cube root |
1 | \(1^3 = 1\) | \(\sqrt[3]{1} = 1\) | 11 | \(11^3 = 1331\) | \(\sqrt[3]{1331} = 11\) |
2 | \(2^3 = 8\) | \(\sqrt[3]{8} = 2\) | 12 | \(12^3 = 1728\) | \(\sqrt[3]{1728} = 12\) |
3 | \(3^3 = 27\) | \(\sqrt[3]{27} = 3\) | 13 | \(13^3 = 2197\) | \(\sqrt[3]{2197} = 13\) |
4 | \(4^3 = 64\) | \(\sqrt[3]{64} = 4\) | 14 | \(14^3 = 2744\) | \(\sqrt[3]{2744} = 14\) |
5 | \(5^3 = 125\) | \(\sqrt[3]{125} = 5\) | 15 | \(15^3 = 3375\) | \(\sqrt[3]{3375} = 15\) |
6 | \(6^3 = 216\) | \(\sqrt[3]{216} = 6\) | 16 | \(16^3 = 4096\) | \(\sqrt[3]{4096} = 16\) |
7 | \(7^3 = 343\) | \(\sqrt[3]{343} = 7\) | 17 | \(17^3 = 4913\) | \(\sqrt[3]{4913} = 17\) |
8 | \(8^3 = 512\) | \(\sqrt[3]{512} = 8\) | 18 | \(18^3 = 5832\) | \(\sqrt[3]{5832} = 18\) |
9 | \(9^3 = 729\) | \(\sqrt[3]{729} = 9\) | 19 | \(19^3 = 6859\) | \(\sqrt[3]{6859} = 19\) |
10 | \(10^3 = 1000\) | \(\sqrt[3]{1000} = 10\) | 20 | \(20^3 = 8000\) | \(\sqrt[3]{8000} = 20\) |
Register for free to see more content