
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoCross multiplication method or Equations reducible to the linear form.
The cross multiplication method is one of the methods to solve an equation. If the given equation is not in a linear polynomial form, we use the cross multiplication method of solving.
Let's understand this concept with an example.
Solve:
The given equation is . This is not in linear polynomial form and also the equation contains variable on both sides. Now apply the cross multiplication rule in this equation.
Step I)
Multiply the numerator in LHS \((2x+4)\) by the denominator in RHS \((10)\).
That is .
Step II)
Multiply the RHS numerator \(x+4\) by the LHS denominator \(2\).
That is .
These steps are explained in the figure given below.
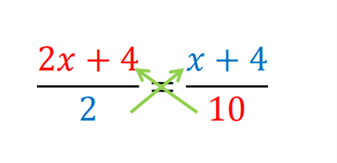
Step III)
Simplify both the sides of the equation.
Step IV)
Now transpose the \(40\) to \(RHS\) side and transpose the variable \(2x\) in \(RHS\) to \(LHS\).
Step V)
Now use the linear equation rule. That is divide by 18 on both sides of the equation.
Therefore the solution for the equation is \(x = -2\).
Let's summarize what we have learned here:
Steps for cross multiplication:
1. Multiply the numerator in LHS by the denominator in RHS.
2. After multiply the RHS numerator by the LHS denominator.
3. Simplify both the sides of the equation.
4. Transpose the constant and variable to \(RHS\) and \(LHS\) respect to the simplified equation.
5. Now use the linear equation rules (Addition, Subtraction, Multiply, Divide - to both sides) to find the solution of the given equation.