PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoIf the side of a polygon is extended, the angle formed outside the polygon is the exterior angle.
The sum of all the exterior angles of a polygon is \(360°\).
Geometrical approach:
When all of the angles of a convex polygon converge or pushed together, they form one angle called one complete turn (Perigon angle), which measures \(360\) degrees.
If the sides of the convex polygon are increased or decreased, the sum of all of the exterior angles is still \(360\) degrees. More sides can be added to the polygon and they will still form \(360°\).
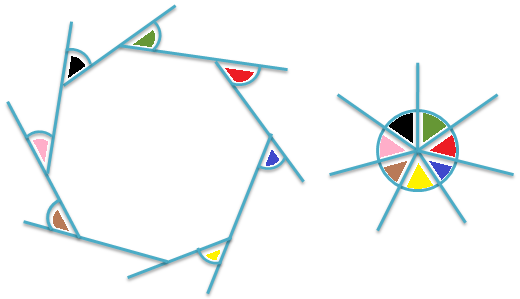
Therefore, the number of sides does not change the sum of the exterior angles of a convex polygon.
Algebraic approach:
For any polygon, exterior angle \(+\) interior adjacent angle \(= 180°\)
So, if the polygon has n sides, then:
Sum of all exterior angles \(+\) Sum of all interior angles \(= n × 180°\)
So, the sum of all exterior angles \(= n × 180°\) \(-\) Sum of all interior angles
Sum of all exterior angles \(= n × 180° - (n -2) × 180°\)
\(=\) \(n × 180°\) \(- n × 180°\) \(+ 2 × 180°\)
\(=\) \(180°n\) \(- 180°n\) \(+ 360°\)
\(= 360°\)
Therefore, we conclude that the sum of all the exterior angles of the polygon having \(n\) sides \(=\) \(360°\).
We know that 'a regular polygon is a polygon whose all sides and all angles are equal. Thus, a regular polygon is both equiangular and equilateral'.
As all the angles are equal in a regular polygon, each exterior angle of a polygon is , where \(n\) is the number of sides.
Alternatively, we can find the number of sides of a regular polygon if we know the exterior angle of it.
The number of sides of a regular polygon \(n = \).
Important!
- The sum of measures of all the exterior angles of a polygon is \(360°\).
- Each exterior angle of a regular polygon is , where \(n\) is the number of sides.
- The number of sides of a regular polygon \(n =\) .
- The sum of all the exterior angles formed by producing the sides of a convex polygon in the same order is equal to four right angles (\(4×90°\) \(= 360°\)).
Register for free to see more content