PDF chapter test TRY NOW
Now recall the angle sum property of a triangle that we studied earlier.
The sum of the measure of three angles of a triangle is \(180°\).
Proof:
Consider a triangle \(ABC\) with interior angles measures \(∠1\), \(∠2\) and \(∠3\).
Draw a line \(DE\) parallel to \(BC\).
Now the angle formed by the parallel line \(DE\) with the triangle \(ABC\) is \(∠4\) and \(∠5\).
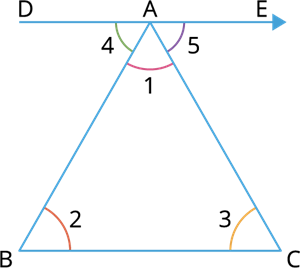
Since \(DE\) is parallel to \(BC\), using the alternate interior angle property \(∠2\) must equal to \(∠4\). Similarly, \(∠3\) must be equal to \(∠5\).
That is \(∠2 =∠4\) and \(∠3=∠5\). As \(DE\) is a straight line, \(∠5\) and \(∠CAD\) are linear pairs (Pair of adjacent supplementary angles).
\(∠5 + ∠CAD = 180°\) .
That is, \(∠5 + ∠1 + ∠4 = 180°\).
Equivalently, \(∠1 + ∠2 + ∠3 = 180°\).
It states that the total measures of the three angles of a triangle is \(180°\).
Let's extend the angle sum property to the quadrilateral.
The sum of all the angles of a quadrilateral is \(360°\).
Proof:
Let \(ABCD\) be a quadrilateral.
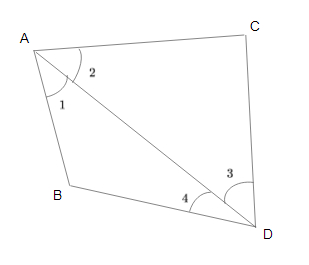
Cut the quadrilateral into two triangles by drawing one of its diagonals \(AC\).
It is obvious from the figure that \(∠1+∠2 =∠A\) and \(∠3+∠4 =∠C\).
We know that the sum of all the angles of a triangle is \(180°\).
Consider the triangle \(ABC\).
\(∠1 + ∠4 + ∠B =180°\).
and \(∠2 + ∠3 + ∠D =180°\).
Adding the above equations will result as follows:
\(∠1 + ∠4\) \(+ ∠B\) \(+ ∠2\) \(+ ∠3\) \(+ ∠D\) \(=\) \(180° + 180°\).
Arranging the angles in order becomes:
\((∠1 + ∠2)\) \(+ ∠B +\) \((∠3 + ∠4)\) \(+ ∠D\) \(= 360°\).
Substitute the known values \(∠1+∠2 =∠A\) and \(∠3+∠4 =∠C\),
\(∠A\) \(+ ∠B\) \(+ ∠C\) \(+ ∠D\) \(= 360°\).
Thus, the sum of the angles of a quadrilateral is \(360°\).
Register for free to see more content