PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoAngles at the circumference on the same segment
Theorem: Angles in the same segment of a circle are equal.
Explanation:
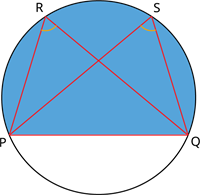
The theorem states that angles in the same segment of the circle are equal. In the given circle, the angles \(\angle PRQ\) and \(\angle PSQ\) are equal as they lie on the same segment (i.e.) \(\angle PRQ = \angle PSQ\).
Proof of the theorem:
Consider a circle with centre \(O\) and chord \(PQ\).
Let \(R\) and \(S\) be any two points on the circumference of the circle lying on the same segment of the circle.
Join the endpoints of the chord \(PQ\) with the centre \(O\).
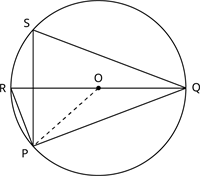
We know that, according to the theorem, the angle subtended by an arc of the circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.
This implies, \(\frac{1}{2} \angle POQ\) \(=\) \(\angle PRQ\) \(……\) \(\text{equation }(1)\)
Similarly, \(\frac{1}{2} \angle POQ\) \(=\) \(\angle PSQ\) \(……\) \(\text{equation }(2)\)
From equation \((1)\) and \((2)\), we have:
\(\angle PRQ\) \(=\) \(\angle PSQ\)
Example:
Find the unknown angles \(x\) and \(y\) in the given figure, where \(O\) is the centre of the circle.
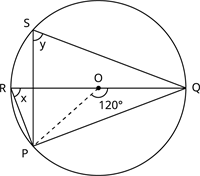
Solution:
According to the theorem, the angle subtended by an arc of the circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.
This implies:
\(\angle PRQ\) \(=\) \(\frac{1}{2} \angle POQ\)
\(x\) \(=\) \(\frac{1}{2} \times 120^{\circ}\)
\(=\) \(60^{\circ}\)
Also, by the theorem, angles in the same segment of a circle are equal.
Hence, \(\angle PRQ\) \(=\) \(\angle PSQ\).
So, \(x\) \(=\) \(y\).
Therefore, \(y\) \(=\) \(60^{\circ}\).
Converse of the theorem: If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle (i.e. they are concyclic).
Explanation:
The theorem states that if the line segment \(PQ\) subtends equal angles at the points \(R\) and \(S\) on the same side of the line containing the segment \(PQ\) then the four points \(P\), \(Q\), \(R\) and \(S\) lie on the circle.
Proof of the theorem:
Consider a line segment \(QR\) which subtends equal angles at the points \(P\) and \(S\) on the same side of the line segment.
That is \(\angle QPR\) \(=\) \(\angle QSR\). \(……(1)\)
We need to prove that the points \(P\), \(Q\), \(R\) and \(S\) lie on the circle. In other words to prove that the points \(P\), \(Q\), \(R\) and \(S\) are concyclic.
Draw a circle through the points \(P\), \(Q\) and \(R\).
Suppose that the circle does not pass through \(S\).
Then assume that the circle intersect \(QS\) at some point \({S}'\).
By the assumption, the points (P\), \(Q\), \(R\) and \({S}'\) lie on the circle.
Hence by the theorem angles in the same segment of a circle are equal.
So, we have \(\angle QPR\) \(=\) \(\angle Q{S}'R\). \(……(2)\)
From equation \((1)\) and \((2)\), \(\angle QSR\) \(=\) \(\angle Q{S}'R\). \(……(3)\)
This is possible only if the points \(S\) and \({S}'\) coincide.
Now consider the triangle \(RS{S}'\).
By the known theorem, exterior angle of a triangle is equal to the sum of the interior opposite angles.
So, \(\angle Q{S}'R\) \(=\) \(\angle {S}'SR\) \(+\) \(\angle SR{S}'\).
Here \(\angle {S}'SR\) \(=\) \(\angle QSR\).
Thus, \(\angle Q{S}'R\) \(=\) \(\angle QSR\) \(+\) \(\angle SR{S}'\). \(……(4)\)
Substitute equation \((3)\) in \((4)\) as follows:
\(\angle QSR\) \(=\) \(\angle QSR\) \(+\) \(\angle SR{S}'\)
\(\angle SR{S}'\) \(=\) \(0\).
The angle measure between the line segments \(RS\) and \(R{S}'\) is zero implies that the points \({S}'\) and \(S\) coincide.
Therefore, the points \(P\), \(Q\), \(R\) and \(S\) lie on the circle.
Register for free to see more content