PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoPerpendicular from the Centre to a Chord
Theorem: The perpendicular from the centre of a circle to a chord bisects the chord.
Explanation:
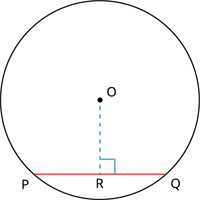
The theorem states that if \(O\) is the centre and \(PQ\) is the chord, then the perpendicular \(OR\) from the centre \(O\) to the chord \(PQ\) bisects the chord \(PQ\) (i.e.) \(PR = RQ\).
Example:
The chord of length \(24 cm\) is drawn from a perpendicular distance of \(9 cm\) from the centre of the circle. Find the radius of the circle.
Solution:
The pictorial representation of the given question is as follows:
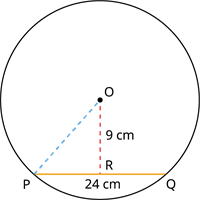
Given the distance from the centre of the circle \(=\) \(9 cm\)
The length of the chord \(=\) \(24 cm\).
Here, \(\angle ORP = 90^{\circ}\).
Therefore, by the theorem, we have:
\(PR = RQ\)
\(=\)
\(=\) 12 \(cm\)
Consider the triangle \(OPR\):
By the known Pythagoras theorem:
\(\text{Hypotenuse side}^{2} = \text{Adjacent side}^{2} + \text{Opposite side}^{2}\)
Let's find the length of \(OP\) as follows:
\(OP^{2} = OR^{2} + RP^{2}\)
\(= 9^{2} + 12^{2}\)
\(= 81 + 144\)
\(= 225\)
Thus, \(OP = \sqrt{225}\)
\(= 15\) \(cm\)
Therefore, the radius of the circle is \(15\) \(cm\).
Converse of the theorem: The line drawn through the centre of the circle to bisect a chord is perpendicular to the chord.
Explanation:
The theorem states that if \(O\) is the centre and \(R\) is the mid-point of the chord \(PQ\), the line joining the centre \(O\) and the mid-point \(R\) is perpendicular to the chord \(PQ\).
Proof of the theorem:
Consider a circle with centre \(O\) and a chord \(PQ\) as follows:
Draw a line \(OR\) joining the centre and the mid-point \(R\) of the chord \(PQ\).
Join the points \(OP\) and \(OQ\).
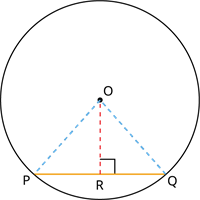
Here, \(OP\) and \(OQ\) are radius. So, they are equal.
Since \(R\) is the mid-point, the sides \(PR = RQ\).
Also, the side \(OR\) is common to the triangle \(ORP\) and \(ORQ\).
Therefore, by the RHS rule (In two right-angled triangles, if the length of the hypotenuse and one side of one triangle is equal to the length of the hypotenuse and corresponding side of the other triangle, then the two triangles are congruent), the triangles \(ORP\) and \(ORQ\) are congruent.
By the congruency the corresponding parts of the triangles are equal. So, \(\angle ORP = \angle ORQ\).
It is observed that \(\angle ORP\) and \(\angle ORQ\) are linear pairs.
This implies:
\(\angle ORP\) \(+\) \(\angle ORQ\) \(=\) \(180^{\circ}\)
\(2 \angle ORP\) \(=\) \(180^{\circ}\)
\(\angle ORP\) \(=\) \(\frac{180^{\circ}}{2}\)
\(=\) \(90^{\circ}\)
Since \(\angle ORP = \angle ORQ = 90^{\circ}\) we say that \(OR \perp PQ\).
Therefore, the line drawn through the centre of the circle to bisect a chord is perpendicular to the chord.
Example:
Find the measure of the angle between the line joining the centre of the circle and the mid-point of the chord of the circle.
Solution:
By the theorem, the line joining the centre of the circle and the midpoint of a chord is perpendicular to the chord.
So, the line from the centre of the circle and the midpoint of a chord are perpendicular to each other.
That is, the angle between the line from the centre to the chord is \(90^{\circ}\).
Therefore, the measure of the angle between the line joining the centre of the circle and the mid-point of the chord of the circle is \(90^{\circ}\).
Register for free to see more content