UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreCyclic Quadrilateral
A four-sided figure inscribed in a circle such that all its vertices lie on the circumference of the circle is said to be a cyclic quadrilateral.
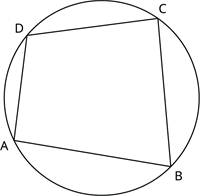
Theorem: The sum of either pair of opposite angles of a cyclic quadrilateral is \(180^{\circ}\).
Explanation:

The theorem states that the sum of the interior opposite angles of a cyclic quadrilateral is \(180^{\circ}\).
That is, \(\angle A + \angle C = 180^{\circ}\).
And \(\angle B + \angle D = 180^{\circ}\).
Proof of the theorem:
Consider a quadrilateral \(ABCD\) whose vertices lie on the circumference of the circle with centre \(O\).
Connect all the four vertices with centre \(O\) to get four isosceles triangle \(AOB\), \(BOC\), \(COD\) and \(DOA\) where the sides \(OA\), \(OB\), \(OC\) and \(OD\) are the radii.
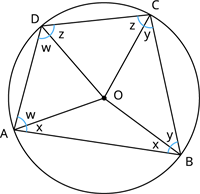
The sum of the angles around the centre of a circle is \(360^{\circ}\).
Also, the sum of all the interior angles of a triangle is \(180^{\circ}\).
Hence:
Adding all the equations we have:
\(2 (\angle w + \angle x + \angle y + \angle z) + \angle O = 4\times180^{\circ}\)
\(2 (\angle w + \angle x + \angle y + \angle z) + 360^{\circ} = 720^{\circ}\)
\(2 (\angle w + \angle x + \angle y + \angle z) = 720^{\circ} - 360^{\circ}\)
\(2 (\angle w + \angle x + \angle y + \angle z) = 360^{\circ}\)
\(\angle w + \angle x + \angle y + \angle z = 180^{\circ}\)
This is rewritten as, \(\angle A + \angle C = 180^{\circ}\).
Similarly, \(\angle B + \angle D = 180^{\circ}\).
Example:
Find the unknown angle \(x\) in the given figure.
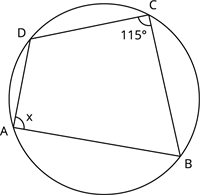
Solution:
By the theorem, opposite angles of a cyclic quadrilateral are supplementary.
This implies:
\(\angle A + \angle C = 180^{\circ}\)
\(x + 115^{\circ} = 180^{\circ}\)
\(x = 180^{\circ} - 115^{\circ}\)
\(x = 65^{\circ}\)
Converse of Theorem: If the sum of a pair of opposite angles of a quadrilateral is \(180^{\circ}\), the quadrilateral is cyclic.
Explanation:
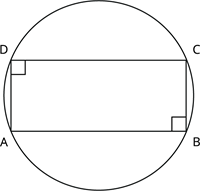
The theorem states that if the sum of the interior opposite angles of any quadrilateral is \(180^{\circ}\), then that quadrilateral is said to be cyclic. Here, in the figure, the sum of the \(\angle A\) and \(\angle C\) is \(180^{\circ}\).
\(90^{\circ} + 90^{\circ} = 180^{\circ}\)
Thus, the quadrilateral \(ABCD\) is cyclic.
Example:
Prove that a square inscribed in a circle is cyclic.
Proof:
Let \(ABCD\) be the square inscribed in a circle.

It is known that every angle of a square is \(90^{\circ}\).
Here \(\angle A + \angle C = 90^{\circ} + 90^{\circ}\)
Implies, \(\angle A + \angle C\) \(=\) \(180^{\circ}\)
Similarly, \(\angle B + \angle D = 90^{\circ} + 90^{\circ}\)
Implies, \(\angle B + \angle D\) \(=\) \(180^{\circ}\)
According to the theorem, the pair of opposite angles of the square is supplementary.
Hence the square inscribed in a circle is cyclic.