PDF chapter test TRY NOW
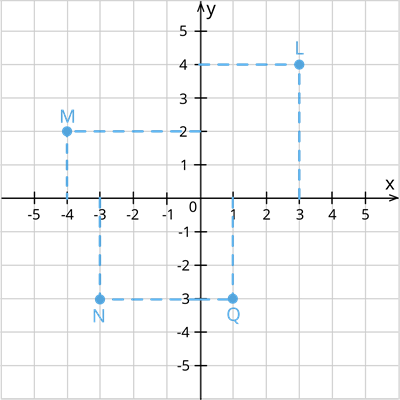
1. The perpendicular distance of the point \(L\) from the \(y\) - axis measured along the positive direction of the \(y\)-axis is \(LX = 4\) units. The perpendicular distance of the point \(L\) from the \(x\)-axis measured along the positive direction of the \(x\)- axis \(OL = 3\) units.
Point L lies in first quadrant in the above graph. Hence its co-ordinates will be represented as (x, y), where \(x = 3\) and \(y = 4\) the co-ordinate of \(L\) in cartesian plane is \((3,4)\).
2. The perpendicular distance of the point \(M\) from the \(y\) - axis measured along the positive direction of the \(y\)-axis is \(MX' = 2\) units. The perpendicular distance of the point \(M\) from the x-axis measured along the negative direction of the \(x\) - axis \(OM = 2\) units.
Point M lies in second quadrant in the above graph. Hence its co-ordinates will be represented as (-x, y), where \(x = 4\) and \(y = 2\) the co-ordinate of M in cartesian plane is \((-4,2)\).
3. The perpendicular distance of the point \(N\) from the \(y\) - axis measured along the negative direction of the \(y\)-axis is \(NX' = 3\) units. The perpendicular distance of the point \(N\) from the \(x\)-axis measured along the negative direction of the \(x\) - axis \(OX' = 2\) units.
Point N lies in third quadrant in the above graph. Hence its co-ordinates will be represented as (-x, -y), where \(x = 2\) and \(y = 3\) the co-ordinate of \(L\) in cartesian plane is \((-2,-3)\).
4. The perpendicular distance of the point \(Q\) from the \(y\) - axis measured along the negative direction of the y-axis is \(QX' = 3\) units. The perpendicular distance of the point \(Q\) from the \(x\)-axis measured along the positive direction of the \(x\) - axis \(OX = 1\) unit.
Point \(Q\) lies in fourth quadrant in the above graph. Hence its co-ordinates will be represented as (x, -y), where \(x = 1\) and \(y = 3\) the co-ordinate of \(L\) in cartesian plane is \((1,-3)\).
Register for free to see more content