UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
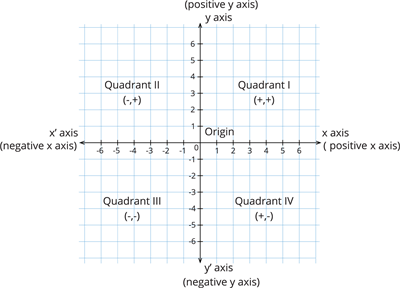
Learn moreThe \(x\) - axis and \(y\) - axis divide the cartesian plane into four regions from the origin. These are called quadrants. They are usually numbered in anticlockwise direction starting from the region bounded by positive \(x\) and \(y\) axis (that is \(OX\)).
Quadrant I:
- Any point located in quadrant \(I\) will have a positive number in the \(x\) - axis and \(y\) - axis.
- That is, \(x > 0\), \(y > 0\).
- The region is \(XOY\). Example:\((2,3)\), \((6,10)\), \((9,12)\)
Quadrant II:
- Any point located in quadrant \(II\) will have a negative number in the \(x\) - axis and a positive number in \(y\) - axis.
- That is, \(x < 0\), \(y > 0\).
- The region is \(X'OY\).Example:\((-3,6)\), \((-2,5)\), \((-15,12)\)
Quadrant III:
- Any point located in quadrant \(III\) will have a negative number in the \(x\) - axis and \(y\) - axis.
- That is, \(x < 0\), \(y < 0\).
- The region is \(X'OY'\).Example:\((-5,-6)\), \((-2,-1)\), \((-8,-10)\)
Quadrant IV:
- Any point located in quadrant \(IV\) will have a positive number in the \(x\) - axis and a negative number in \(y\) - axis.
- That is, \(x > 0\), \(y < 0\).
- The region is \(XOY'\).Example:\((1,-3)\), \((3, -4)\), \((7,-1)\)
Coordinate of a point on the axes:
- If a point lies on the \(x\) - axis, then the coordinate is \((x,0)\). That is, \(y=0\).Example:\((-3,0)\), \((6,0)\), \((1,0)\).
- If a point lies on the \(y\) - axis, then the coordinate is \((0,y)\). That is, \(x=0\). Example:\((0,-1)\), \((0,5)\), \((0,10)\).
Register for free to see more content