UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreIn the earlier classes, we studied about perimeter and area of triangles.
Perimeter \(=\) \(\text{Sum of the three sides of the triangle}\)
Area \(=\) \(\times \ \text{Base} \times \text{Height}\)
Let us discuss how to find the area of different types of triangles in detail.
Area of a right angle triangle:
When the triangle is right angle triangle, we can directly apply the formula and can find the area. Because, right angle triangle have base and height.
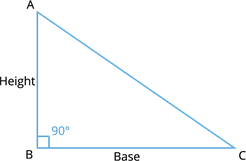
Suppose \(AB = 6 \ cm\), \(BC = 8 \ cm\) and \(AC = 10 \ cm\).
Area \(=\) \(\times \ BC \times AB\)
Area \(=\) \(\times \ 8 \times 6\)
Area \(=\) \(24 \ cm^{2}\)
Area of an equilateral triangle:

To find the area of an equilateral triangle and isosceles triangle:
Step 1: Draw a perpendicular line from the top of the vertex to the base. This line divides the base into two equal halves. Also, divides the triangle into two triangles of equal area.
Step 2: To find the area, we need height \((AD)\). Using Pythagoras theorem, we can find height \((AD)\).
\( \text{Hypotenuse}^{2}\) \(=\) \(\text{Base}^{2}\) \(+ \text{Height}^{2}\)
Step 3: After finding \(AD\), we can find the area of \(\Delta ABD\).
Step 4: Since \(AD\) divides a \(\Delta ABC\) into two equal areas, area of \(\Delta ABD\) and area of \(\Delta ADC\) are same.
Step 5: Thus, adding area of \(\Delta ABD\) and \(\Delta ADC\), we get the area of \(\Delta ABC\).
Area of an isosceles triangle:
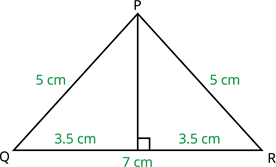
In the same way of finding the area of an equilateral triangle, we can find the area of an isosceles triangle.
Area of a scalene triangle:

For a scalene triangle, we cannot find the height, because all the three sides are different.
In this case, we have a formula called Heron's formula to find the area of triangles.
Important!
Heron's formula can be applied for all type of triangles.