UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreStudy the following real number line.
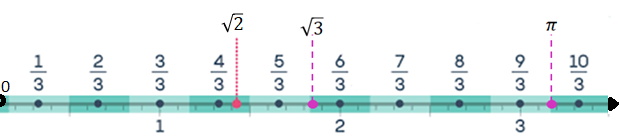
It can be observed from the number line that there are numbers that are not rationals (, , , etc.). Let's discuss such kind of numbers.
And so far, all the numbers you have come across are of the form \(p/q\), where \(p\) and \(q\) are integers and . But there are some numbers which cannot be expressed in \(p/q\) form. We are going to discuss such kind of numbers.
The Pythagoreans in Greece was the first to discover the numbers which were not rational, around \(400 BC\). These numbers are called an irrational number.
An irrational number is a number that cannot be expressed as a fraction \(p/q\), where for any integers \(p\) and \(q\).
Irrational numbers have decimal expansions that neither terminate nor become periodic.
Irrational numbers have decimal expansions that neither terminate nor become periodic.
Important!
As there are infinitely many rationals, so there are infinitely many irrational numbers too.
Some of the irrationals are as follows:
Example:
\(= 1.4142135623730950488…\)
\(= 1.7320508075688772935…\)
\(= 2.23606797749978969…\)
\(= 3.1415926535897932384626433...\)
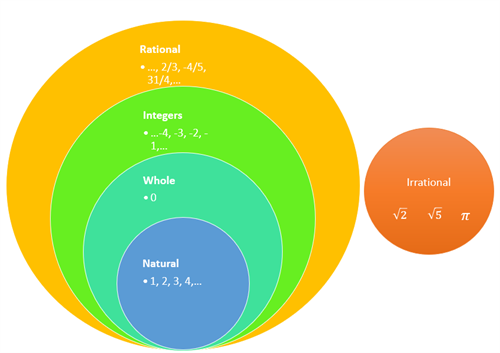
Here come the pictorial forms of the classification of numbers:
Register for free to see more content