UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreReal numbers are the numbers which include both rational and irrational numbers. A real number is denoted by "\(R\)".
Important!
Every real number is either rational or irrational.
German mathematicians, Cantor and Dedekind, discovered that 'Corresponding to every real number, there is a point on the real number line, and corresponding to every point on the number line, there exists a unique real number'.
Let's us study how to represent rational and irrational numbers using the decimal expansions. Then we can extend that to real numbers.
Now we will analyse the decimal expansions of different types of numbers.
Numbers | Value with the help of long division | Nature of the decimal expansion | Type of number |
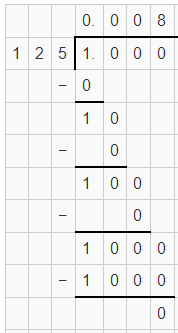 | Terminating expansion. | Rational | |
 | Recurring and non-terminating decimals. | Rational | |
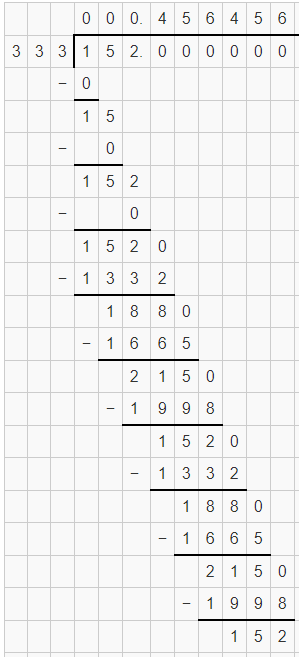 | Recurring and non-terminating decimals. | Rational | |
| In 2019, using the high precision multiplication algorithms of supercomputer \(31.4\) trillion digits of decimals has been predicted. | Non -repeating and non- terminating decimals. | Irrational |
Register for free to see more content