UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreTheorem I:
A diagonal of a parallelogram divides it into two congruent triangles.
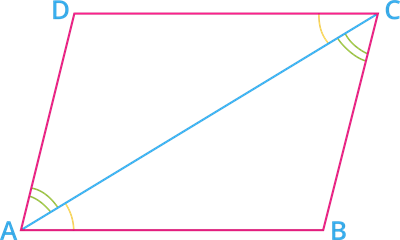
Given: \(ABCD\) is a parallelogram, and \(AC\) is a diagonal.
Diagonal divides the quadrilateral into two triangles \(ABC\) and \(ADC\).
To prove: \(\Delta ABC \cong \Delta CDA\)
Proof: We know that "the opposite sides of a parallelogram are parallel".
\(AB \ || \ DC\) and \(BC \ || \ AD\)
Since \(AB \ || \ DC\) and \(AC\) is a transversal,
\(\angle BAC = \angle DCA\) [alternate interior angles] - - - - - (I)
Also, \(BC \ || \ AD\) and \(AC\) is a transversal,
\(\angle BCA = \angle DAC\) [alternate interior angles] - - - - - (II)
In \(\Delta ABC\) and \(\Delta CDA\):
\(\angle BAC = \angle DCA\) [from (I)]
\(\angle BCA = \angle DAC\) [from (II)]
\(AC = AC\) [Common side]
Thus, \(\Delta ABC \cong \Delta CDA\) [by \(ASA\) congruence rule].
Therefore, the diagonal of a parallelogram divides it into two congruent triangles.
Theorem II:
In a parallelogram, opposite sides are equal.
Given: \(ABCD\) is a parallelogram, and \(AC\) is a diagonal.
Diagonal divides the quadrilateral into two triangles \(ABC\) and \(ADC\).
To prove: \(AB = CD\) and \(BC = AD\)
Proof: We know that "the opposite sides of a parallelogram are parallel".
\(AB \ || \ DC\) and \(BC \ || \ AD\)
Since \(AB \ || \ DC\) and \(AC\) is a transversal,
\(\angle BAC = \angle DCA\) [alternate interior angles] - - - - - (I)
Also, \(BC \ || \ AD\) and \(AC\) is a transversal,
\(\angle BCA = \angle DAC\) [alternate interior angles] - - - - - (II)
In \(\Delta ABC\) and \(\Delta CDA\):
\(\angle BAC = \angle DCA\) [from (I)]
\(\angle BCA = \angle DAC\) [from (II)]
\(AC = AC\) [Common side]
Thus, \(\Delta ABC \cong \Delta CDA\) [by \(ASA\) congruence rule].
Corresponding parts of congruent triangles are equal.
\(\Rightarrow AB = DC\) and \(BC = AD\).
Therefore, the opposite sides of a parallelogram are equal.
Theorem III:
If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
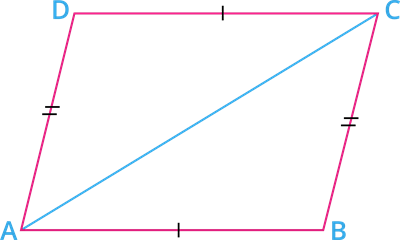
Given: \(ABCD\) is a quadrilateral, where \(AB = DC\) and \(BC = AD\).
Construction: Join the diagonal \(AC\).
To prove: \(ABCD\) is a parallelogram.
Proof: In \(\Delta ABC\) and \(\Delta CDA\):
\(AB = DC\) [Given]
\(BC = AD\) [Given]
\(AC = AC\) [Common side]
Thus, \(\Delta ABC \cong \Delta CDA\) [by \(SSS\) congruence rule].
\(\implies \angle BAC = \angle DCA\) [by CPCT] - - - - (I)
\(\implies \angle BCA = \angle DAC\) [by CPCT] - - - - (II)
These angles are alternate interior angles.
We know that "the alternate interior angles are equal only when the lines are parallel".
So, \(AB \ || \ DC\) and \(BC \ || \ AD\).
Hence, \(ABCD\) is a parallelogram.
Important!
CPCT - Corresponding Parts of Congruence Triangles
Register for free to see more content