PDF chapter test TRY NOW
Theorem IV
In a parallelogram, opposite angles are equal.
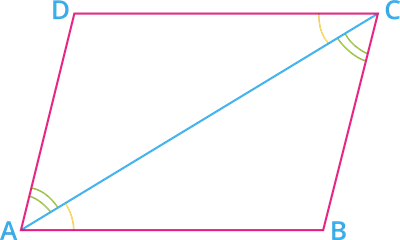
Given: \(ABCD\) is a parallelogram.
Construction: Join the diagonal \(AC\).
To prove: \(\angle A = \angle C\) and \(\angle B = \angle D\)
Proof: We know that "opposite sides of a parallelogram are parallel".
\(AB \ || \ CD\) and \(BC \ || \ AD\)
Since \(AB \ || \ CD\) and \(AC\) is a transversal.
\(\angle BAC = \angle DCA\) [alternate interior angles] - - - - - (I)
Also, \(AD \ || \ BC\) and \(AC\) is a transversal.
\(\angle DAC = \angle BCA\) [alternate interior angles] - - - - - (II)
Add equations (I) and (II).
\(\angle BAC + \angle DAC = \angle DCA + \angle BCA\)
\(\angle BAD = \angle DCB\)
That is, \(\angle A = \angle C\) - - - - - - (III)
Now, join the diagonal \(BD\).
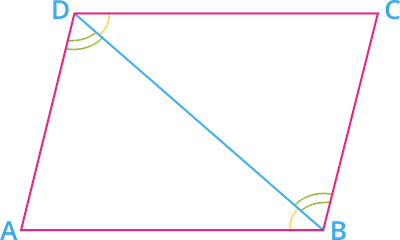
Since \(AB \ || \ CD\) and \(BD\) is a transversal.
\(\angle ABD = \angle CDB\) [alternate interior angles] - - - - - (IV)
Also, \(AD \ || \ BC\) and \(BD\) is a transversal.
\(\angle CBD = \angle ADB\) [alternate interior angles] - - - - - (V)
Add equations (IV) and (V).
\(\angle ABD + \angle CBD = \angle CDB + \angle ADB\)
\(\angle ABC = \angle ADC\)
That is, \(\angle B = \angle D\) - - - - - - (VI)
From (III) and (VI), we get:
The opposite angles of a parallelogram are equal.
Theorem V
If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
Given: \(ABCD\) is a quadrilateral, where \(\angle A = \angle C\) and \(\angle B = \angle D\).
To prove: \(ABCD\) is a parallelogram.
Proof: By angle sum property of a quadrilateral:
\(\angle A + \angle B + \angle C + \angle D = 360^\circ\)
\(\angle A + \angle B + \angle A + \angle B = 360^\circ\) (Using given)
\(2 \angle A + 2 \angle B = 360^\circ\)
\(2 ( \angle A + \angle B) = 360^\circ\)
\(\angle A + \angle B = 180^\circ\) - - - - (I)
Now, consider \(AB\) is the transversal for the lines \(AD\) and \(BC\).
\(\angle A\) and \(\angle B\) are interior angles on the same side of transversal line \(AB\).
"Two lines cut by a transversal are parallel if and only if interior angles on the same side of the transversal are \(180^\circ\)".
Since \(\angle A + \angle B = 180^\circ\)
\(\Rightarrow AD \ || \ BC\) - - - - - (II)
Similarly, \(\angle A + \angle B + \angle C + \angle D = 360^\circ\)
\(\angle A + \angle D + \angle A + \angle D = 360^\circ\) (Using given)
\(2 \angle A + 2 \angle D = 360^\circ\)
\(2 ( \angle A + \angle D) = 360^\circ\)
\(\angle A + \angle D = 180^\circ\) - - - - (III)
Similarly, \(AD\) is the transversal for lines \(AB\) and \(DC\).
\(\angle A\) and \(\angle D\) are interior angles on the same side of transversal line \(AD\).
"Two lines cut by a transversal are parallel if and only if interior angles on the same side of the transversal are \(180^\circ\)".
Since \(\angle A + \angle D = 180^\circ\)
\(\Rightarrow AB \ || \ DC\) - - - - - (IV)
From equations (II) and (IV), we get:
\(AD \ || \ BC\) and \(AB \ || \ DC\)
Both pair of opposite sides are parallel.
Therefore, \(ABCD\) is a parallelogram.
Register for free to see more content