
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoTheorem VIII
A quadrilateral is a parallelogram if a pair of opposite sides is equal and parallel.
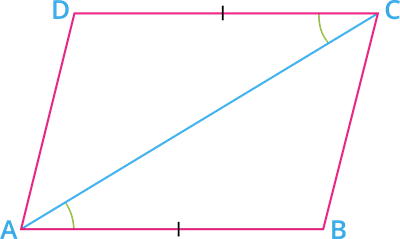
Given: \(ABCD\) is a quadrilateral, where \(AB = CD\) and \(AB \ || \ CD\).
To prove: \(ABCD\) is a parallelogram.
Proof: In \(\Delta ADC\) and \(\Delta CBA\):
\(AB = CD\) [Given]
\(\angle BAC = \angle ACD\) [Alternate interior angles]
\(CA = CA\) [Common side]
Therefore, \(\Delta ADC \cong \Delta CBA\) [by \(ASA\) congruence criterion].
\(\Rightarrow AD = BC\) [by CPCT] - - - - - (I)
We have, \(\angle BAC = \angle ACD\).
These are alternate angles.
The alternate interior angles theorem states that, "the alternate interior angles are congruent when the transversal intersects two parallel lines".
Here, \(AC\) is the transversal line for the lines \(AD\) and \(BC\).
So, \(AD \ || \ BC\) - - - - - (II)
From (I) and (II), we get:
\(AD \ || \ BC\) and \(AD = BC\)
Thus, both pair of opposite sides are equal and parallel.
Therefore, \(ABCD\) is a parallelogram.