PDF chapter test TRY NOW
Theorem VI
The diagonals of a parallelogram bisect each other.
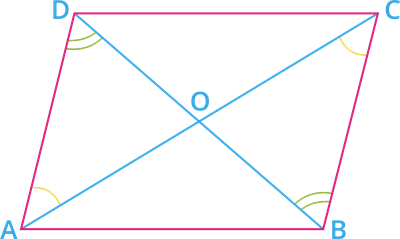
Given: \(ABCD\) is a parallelogram, where \(AC\) and \(BD\) are diagonals. \(O\) is the point of intersection of diagonals.
To prove: \(OA = OC\) and \(OB = OD\)
Proof: We know that "opposite sides of a parallelogram are parallel".
\(AD \ || \ BC\) and \(AB \ || \ CD\)
Since \(AD \ || \ BC\) and \(AC\) is a transversal.
\(\angle DAC = \angle BCA\) [alternate interior angles]
\(\Rightarrow \angle DAO = \angle BCO\) - - - - - - (I)
Also, \(AD \ || \ BC\) and \(BD\) is a transversal.
\(\angle ADB = \angle CBD\) [alternate interior angles]
\(\Rightarrow \angle ADO = \angle CBO\) - - - - - - (II)
In \(\Delta AOD\) and \(\Delta COB\):
\(\angle DAO = \angle BCO\) [from (I)]
\(\angle ADO = \angle CBO\) [from (II)]
\(\angle AOD = \angle COB\) [vertically opposite angles]
Therefore, \(\Delta AOD \cong \Delta COB\) [by \(AAA\) congruence rule].
Corresponding parts of congruence triangles are equal.
\(OA = OC\) and \(OD = OB\)
Hence, proved.
Theorem VII
If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
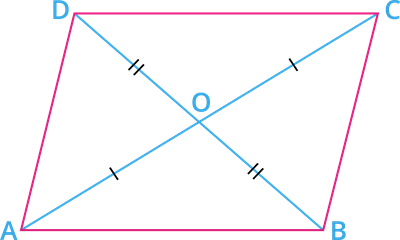
Given: \(ABCD\) is a quadrilateral, where \(AC\) and \(BD\) are diagonals intersect at \(O\).
\(OA = OC\) and \(OB = OD\)
To prove: \(ABCD\) is a parallelogram.
Proof: In \(\Delta AOD\) and \(\Delta COB\):
\(OA = OC\) [Given]
\(\angle AOD = \angle BOC\) [vertically opposite angles]
\(OD = OB\) [Given]
Therefore, \(\Delta AOD \cong \Delta COB\) [by \(SAS\) congruence rule].
\(\Rightarrow \angle ADO = \angle CBO\) [by CPCT]
\(\angle ADO\) and \(\angle CBO\) are alternate interior angles.
The alternate interior angles theorem states that, "the alternate interior angles are congruent when the transversal intersects two parallel lines".
Here, \(BD\) is the transversal for the lines \(AD\) and \(BC\).
Since \(\angle ADO = \angle CBO\)
\(\Rightarrow AD \ || \ BC\) - - - - - (I)
Similarly, in \(\Delta AOB\) and \(\Delta COD\):
\(OA = OC\) [Given]
\(\angle AOB = \angle COD\) [vertically opposite angles]
\(OB = OD\) [Given]
Therefore, \(\Delta AOB \cong \Delta COD\) [by \(SAS\) congruence criterion].
\(\Rightarrow \angle BAO = \angle DCO\) [by CPCT]
\(\angle BAO\) and \(\angle DCO\) are alternate interior angles.
\(AC\) is the transversal lines for the lines \(AB\) and \(CD\).
Since \(\angle BAO = \angle DCO\)
\(\Rightarrow AB \ || \ CD\) - - - - - (II)
From equations (I) and (II), we get:
\(AB \ || \ CD\) and \(AD \ || \ BC\).
Therefore, \(ABCD\) is a parallelogram.
