UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreSphere:
A sphere is a three-dimensional figure obtained by the revolution of a semicircle about its diameter as an axis.
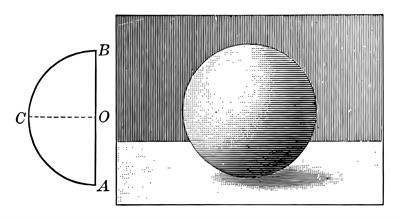
From the figure, \(ACB\) is a semicircle. If we rotate the semicircle \(ACB\) with diameter \(AB\) as an axis, we get the three-dimensional object sphere.
Properties of a sphere:
1. Sphere is made of all the points in the space which are equidistant from the fixed point called the centre.
2. Distance between the centre to the edge of the sphere is called the radius \((r)\) of the sphere.
3. Distance between any two points on a sphere through the centre is called the diameter \((d)\) of the sphere.
4. Diameter \(=\) \(2 \ \times\) radius
Surface area of a sphere:
Surface area of a sphere \(=\) \(4 \ \times\) Area of a circle
\(=\) \(4 \times \pi r^2\)
Surface area of a sphere \(=\) \(4 \pi r^2\)sq. units.
Register for free to see more content