Volume of hemisphere — lesson. Mathematics CBSE, Class 9.

PDF chapter test TRY NOW

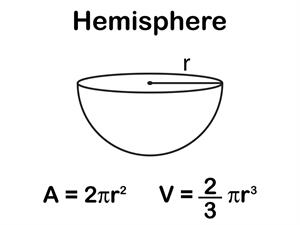
Hemisphere:

A one half of a sphere is called a hemisphere.

Volume of a hemisphere:

Let \(r\) be the radius of a sphere.

Volume of a hemisphere \(=\)

\frac{1}{2}

\(\times\) Volume of a sphere

\(=\)

\frac{1}{2} \times (\frac{4}{3} π r^{3})

\(=\)

\frac{2}{3} π r^{3}

Volume of a hemisphere \(=\)

\frac{2}{3} π r^{3}

cu. units

Example:

The radius of the hemisphere is \(14 \ cm\). Find the volume of the hemisphere in grams if \(1 \ cm^3 = 0.4 \ g\).

Solution:

Radius of the hemisphere \((r)\) \(=\) \(14 \ cm\)

Volume of the hemisphere \(=\)

\frac{2}{3} π r^{3}

cu. units

\(=\)

\frac{2}{3} \times \frac{22}{7} \times 14^{3}

\(=\)

\frac{2}{3} \times \frac{22}{7} \times 14 \times 14 \times 14

\(=\) \(5749.33\) \(cm^3\)

Now, convert \(cm^3\) to \(g\).

\(1 \ cm^3\) \(=\) \(0.4 \ g\)

\(5749.33 \ cm^3\) \(=\) \(5749.33 \times 0.4\) \(=\) \(2299.732 \ g\)

Therefore, the volume of the hemisphere is \(2299.732 \ g\).

Important!

The value of \(\pi\) should be taken as

\frac{22}{7}

unless its value is shared in the problem.

Did you find an error?

2. Volume of hemisphere