
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoEarlier, we explored the linear equation. Where we learned 'what is an equation, and how we can solve it using various methods'.
Now we recall about equation; then we jump into the exciting topic called inequation.
Now we recall about equation; then we jump into the exciting topic called inequation.
Equation: The equation is a statement of equality that contains one or more unknown value or variables.
Example:
Consider the equation \(2x + 4 = 10\);
If we substitute \(x = 4\) we can get \(LHS = RHS\). Therefore, the solution of \(x\) for this equation is \(4\).
Are you wondering how this equation concept related to the inequation?
Let me make it clear for you.
In the above equation, we can notice that \(LHS\) \((2x + 4)\) and \(RHS\) \((10)\) are equal, whereas, in the inequation, it does not plain and simple.
When an algebraic expression is equated on both sides, it will be called an equation; if it is not equated, it is known as inequation or inequality.
In the above equation, we can notice that \(LHS\) \((2x + 4)\) and \(RHS\) \((10)\) are equal, whereas, in the inequation, it does not plain and simple.
When an algebraic expression is equated on both sides, it will be called an equation; if it is not equated, it is known as inequation or inequality.
Inequation:
Let us see a situation to understand this concept.
Rajiv wanted to get a voter ID card. But as per norms, one should attain an age of \(18\) to get a voter ID card. But Rajiv's age is lesser than \(18\).
If we take Rajiv's age as \((x)\) and write the above statement in an algebraic inequation, we get:
\(x < 18\). That means Rajiv's age is lesser than \(18\).
If Rajiv's age is \(18\), then the expression will be \( x = 18\). But it does not.
Since the expression \(x < 18\) is not an equal, this is not an equation; it is called inequation.
1. An algebraic statement that shows two algebraic expressions being unequal is called an algebraic inequation.
2. In general, when two expressions are compared, one might be; less than \((<)\), less than or equal to \((≤)\), greater than \((>)\), greater than or equal to \((≥)\) the other.
3. In an inequation, the algebraic expressions are connected by one out of the four signs of inequalities, namely, \(>\), \(≥\), \(<\) and \(≤\).

Now we explore some examples of how we can use the inequation.
Example:
1. Sanjay is older than Riya
Let us consider Sanjay's age as \((x)\), and Riya's age be \((y)\). Since Sanjay is older than Riya, we should use the greater than \((>)\) symbol towards Sanjay.

Therefore, the inequation will be \( x > y\).
2. Veena's monthly income is not more than \(₹50000\).
Consider Veena's salary as \((x)\). Since Veena's salary is not more than \(₹50000\), her salary must be \(₹50000\) or lesser than \(₹50000\).
So, we should use the lesser than equal symbol \((≤)\) in the inequation.
Therefore, the inequation will be \(x ≤ ₹50000\).
Therefore, the inequation will be \(x ≤ ₹50000\).

3. Kavitha said to her father that she would score \(70\) mark or more than \(70\) marks in the coming mathematics exam.
Say the mark she will score is \((x)\). She will score \(70\) mark or more than \(70\) marks; here, we can use greater than equal symbol to denote the inequation.
Hence, the inequation is \(x ≥ 70\) marks.
Some more examples:
Some more examples:
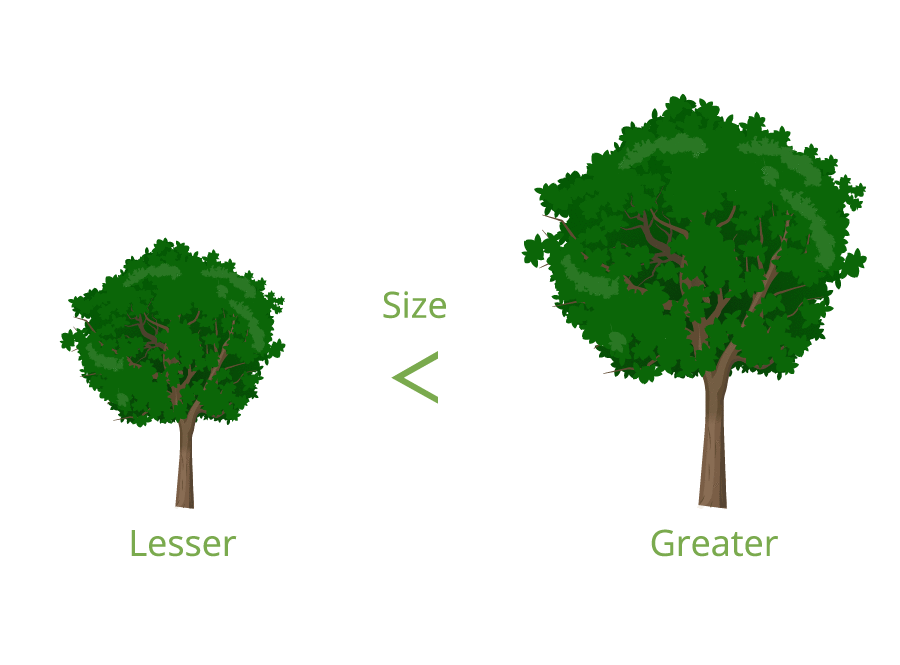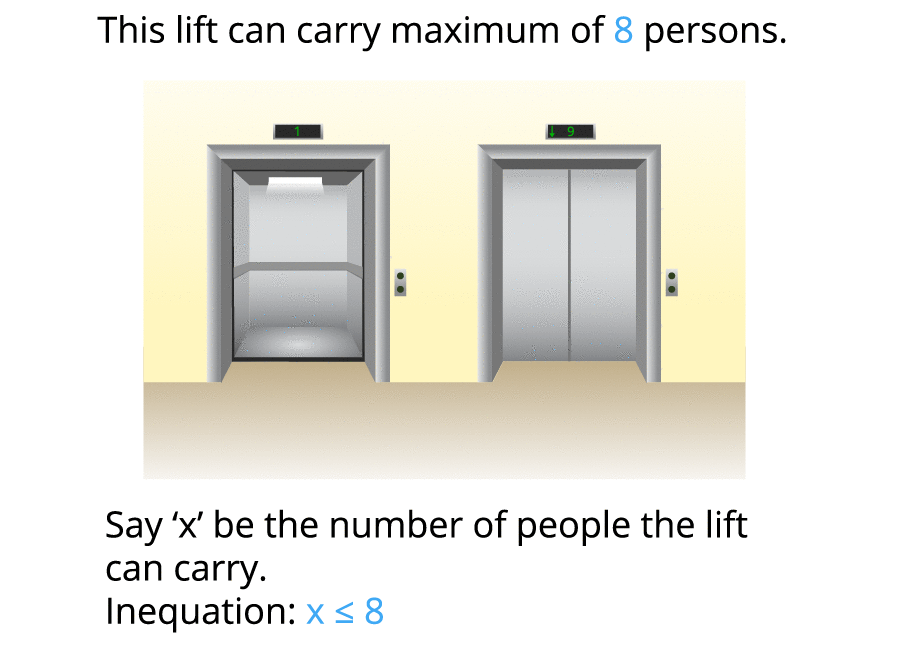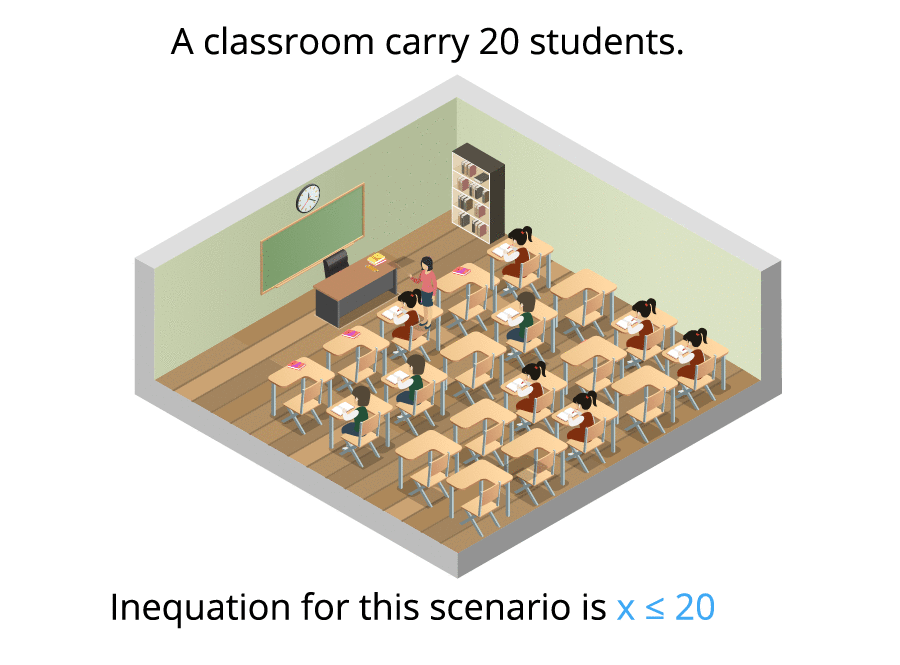
Important!
- \(LHS\) - stands for Left Hand Side
- \(RHS\) - stands for Right Hand Side