PDF chapter test TRY NOW
What is meant by degree of expression?
In an expression, the terms containing the highest power of the variables is called as degree of the expression.
First, let us understand the concept of degree of variables.
Let us consider a square of side length \(x\).
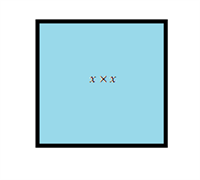
Then, the area of the square \(= x \times x\) \(= x^2\) \(sq. \ units\).
Here, the expression \(x^2\) is a monomial expression, and the highest power of the expression is \(2\) which is obtained by adding the exponents.
Similarly, let us consider a rectangle whose length is \(l\) units and breadth is \(b\) units.
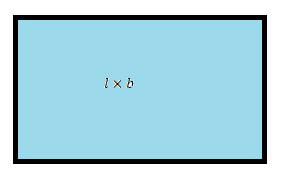
The area of the rectangle \(= l \times b\) \(sq. \ units\)
The expression is \(l^1b^1\). Now, to find the degree of the expression, let us add the powers. Thus, we have, \(1 + 1 =2\).
Hence, the expression \(lb\) has the highest power \(2\), which is obtained by adding the exponents of variable factors.
Example:
1. Find the degree of the expression \(3y^2 + y +2\)
Solution:
The terms in the given expression are \(3y^2\), \(y\) and \(2\). Exponent of the term \(3y^2\) is \(2\), and the exponent of the term \(y\) is \(1\).
Here, the term \(3y^2\) has the highest degree \(2\).
Therefore, the degree of the expression is \(2\).
2. Find the degree of the expression \(2x^2 +3xy^4 +y+6\).
Solution:
The terms in the given expression are \(2x^2\), \(3xy^4\), \(y\) and \(6\).
Exponent of the term \(2x^2\) is \(2\).
Exponent of the term \(3xy^4\) is \(1 + 4 = 5\) (Obtained by adding the variable factors).
Exponent of the term \(y\) is \(1\).
Since, the term \(3xy^4\) has the highest degree \(5\).
Therefore, the degree of the expression is \(5\).
Register for free to see more content