PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoIn direct proportion, two quantities \(x\) and \(y\) are said to increase (or decrease) together in such a way that the ratio of their respective values is constant.
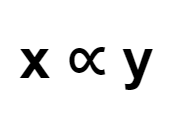
That is to suggest that if \(\frac{x}{y} =\) \(k\) is positive, then \(x\) and \(y\) will differ directly. That is, \(x\) and \(y\) are in direct proportion.
When the quantities \(x\) and \(y\) are in direct proportion, we can write \(=\) . But, where , are values of \(y\) corresponding to the values , of \(x\).
Example:
If \(1\) part of sugar requires \(75 mL\) of water, how much amount of sugar should we mix with \(1800 mL\) of water?
Let the parts of sugar mix with \(1800 mL\) water be \(x\).
Practically, if \(1\) part of a sugar requires \(75 mL\), of water, then \(1800 mL\) of water requires more sugar.
Increase in quantity of water increases the quantity of sugar. So it is in direct proportion.
When the quantities \(x\) and \(y\) are in direct proportion, we can write \(=\) . Where , are values of \(y\) corresponding to the values , of \(x\).
Substitute the known values in the formula.
\(\frac{1}{75}\) \(=\) \(\frac{x}{1800}\)
\(75\) \(x\) \(=\) \(1\) \(1800\)
\(x =\) \(\frac{1800}{75}\)
\(x =\) \(24\)
Hence, \(24\) parts sugar should be mixed with the water of \(1800 mL\).
Register for free to see more content