PDF chapter test TRY NOW
Two quantities \(x\) and \(y\) are found to be inversely proportional when an increase of \(x\) causes \(y\) (and vice versa) to decrease proportionally. The product of their corresponding values remains constant.
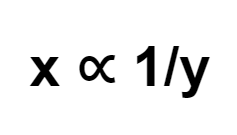
That is, if \(xy = k\), then it is stated \(x\) and \(y\) vary inversely proportional.
When the quantities \(x\) and \(y\) are in indirect proportion, we can write \(=\) or \(=\) . Where , are the values of \(y\) corresponding to the values , of \(x\).
Example:
A farmer has enough food to feed \(20\) hens in his field for \(6\) days. How much longer would the food last if the field contained an additional \(10\) hens?
Let the number of days be \(x\).
Total number of hens \(= 20\) \(+\) \(10 =\) \(30\).
The length of time that food is consumable reduces as hen numbers rise.
As a result, the relationship between the number of hens and the number of days are inversely proportional.
When the quantities \(x\) and \(y\) are in indirect proportion, we can write \(=\) or \(=\) . Where , are the values of \(y\) corresponding to the values , of \(x\).
Substitute the known values.
\(\frac {20}{30}\) \(=\) \(\frac{x}{6}\)
\(\frac {2}{3}\) \(=\) \(\frac{x}{6}\)
\(3\) \(×\) \(x\) \(=\) \(2\) \(×\) \(6\)
\(3x =\) \(12\)
\(x =\) \(\frac{12}{3}\)
\(x =\)\(4\)
Hence, the food will last for four days.
Register for free to see more content