UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreWe might have seen the train tracks many time don't we? Now we are going to see those train tracks with slightly different perspective.
The above not only figure express the intersection of train tracks also about Vertically opposite angles. Now you are wondering what does it mean Vertically opposite angles. Let's explore it.
Vertically opposite angles:
When two lines are intersect each other, the two pairs of non-adjacent angles created which are called vertically opposite angles.
For example, the above train track can be marked with intersecting angle, which we are already familiar with. These intersecting angles
Consider any one among the above angles say, \(∠a\). The angles which are adjacent to \(∠a\) are \(∠b\) and \(∠c\), but \(∠d\) is a non-adjacent angle.
Here \(∠a = ∠d\), because the vertically opposite angles are equal.
Similarly, for the remaining three angles two angles will be adjacent and one angle will be non-adjacent. We can observe that an angle and its non-adjacent angle are just opposite to each other at the point of intersection \(O\) (vertices).
Such angles which are opposite to each other with reference to the vertex are called vertically opposite angles.
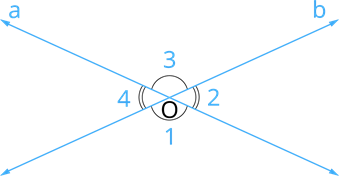
Example:
Here the two lines \(a\) and (b\) are crossing the center \(O\) and making the angles of \(∠1\) , \(∠2\), \(∠3\), and \(∠4\). We can observe that the adjacent angles of \(∠1\) is \(∠2\) and \(∠4\), then the vertically opposite angles of \(∠1\) is \(4\). And the \(∠1 = ∠3 \) are equal, because they vertically opposite angles.
Register for free to see more content