PDF chapter test TRY NOW
Let's learn the types of triangle:
Triangles can be classified based on its sides as well as its angles.
Types of triangles based on its side lengths are as follows.
- Equilateral triangle
- Isosceles triangle
- Scalene triangle
A triangle is an equilateral when all its sides are equal in length.
Example:
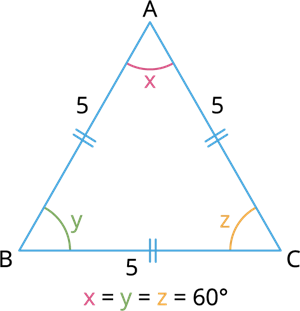
In here, the sides are equal in measure \(AB=BC=CA=5\) units.
A triangle is isosceles when two of its sides are equal in length.
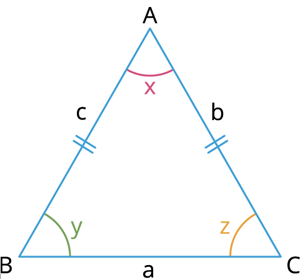
Example:
In here, the two of the sides are equal in measure \(AB=CA=1\) unit and \(BC=√2\) units.
A triangle is a scalene when all the three sides are unequal.
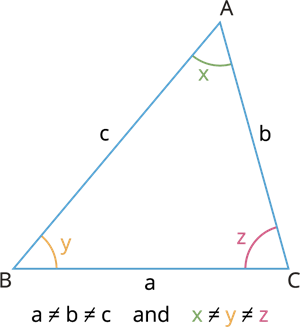
Example:
In here, all the sides are unequal in measure \(AB=7.7, CA=5\) units and \(BC=9\) units.
Types of triangles based on its angles are as follows.
- Acute angled triangle
- Right angle triangle
- Obtuse angled triangle
A triangle is acute angle triangle when all the three of its angle are acute (less than 90°).
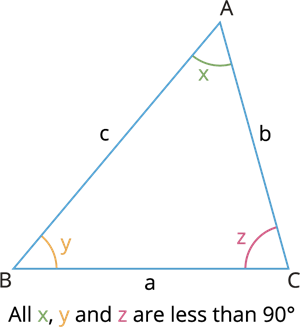
Example:
In here, all the three angles are less than \(90°\). That is, \(∠A=60°, ∠B=50°\) and \(∠C=70°\).
A triangle is right angle triangle when one of its angles is a right angle (90°), and the other two are acute angles (less than 90°).
Example:
In here, one among the angle is \(90°\), and the other two are acute. That is, \(∠A=40°, ∠B=50°\) and \(∠C=90°\).
A triangle is an obtuse angle triangle when one of its angles is an obtuse angle (greater than 90°), and the other two are acute angle (less than 90°).
Example:
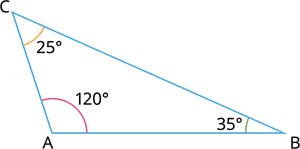
In here, one among the angle greater than \(90°\) and the other two are acute. That is, \(∠A=120°, ∠B=35°\) and \(∠C=25°\).
Register for free to see more content