UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreRight angled triangle:
A triangle is said to be right angled, if one of its angles is \(90^\circ\).
From the examples given above, it is visible that the sides \(BC\), \(QR\), and \(YZ\) are the longest sides. These longest sides are the hypotenuses.
Hypotenuse:
The longest side of a right angled triangle is called a hypotenuse.
Right angle-Hypotenuse-Side (RHS) congruence criterion
The RHS congruence criterion is similar to the SAS congruence criterion.
The only difference is that \(90^\circ\) is the only angle used.
To prove that the two right angled triangles are congruent, it is enough to prove that any one side and the hypotenuse one triangle is congruent to the corresponding side and the hypotenuse of the other triangle.
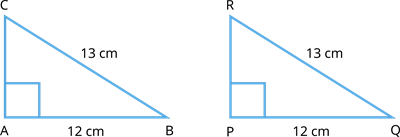
From the figure given above, sides \(AB = PQ = 12\) \(cm\), and the hypotenuses \(BC = QR = 13\)\(cm\).
Since the corresponding sides and the hypotenuses are equal, the triangles \(\triangle ABC\) and \(\triangle PQR\) are congruent.
Important!
Hypotenuses are present only in right angled triangles.
Register for free to see more content