PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoThe congruence principle can be observed in objects around us.
So, it is a no-brainer that it exists in geometrical shapes as well.
A few of the congruences are:
1. Congruence of line segments
2. Congruence of angles
3. Congruence of circles
4. Congruence of polygons
Let us look at each of them in detail.
Congruence of line segments
Two line segments having the same length are said to be congruent line segments. But the positions and the angles at which the two line segments lie need not be the same.
Example:
In here, the line segments \(\overline{AB}\) and \(\overline{CD}\) are in equal length. Hence, they can also be called congruent line segments. They can be written as \(\overline{AB}\) \(\overline{CD}\).
Congruence of angles
Two angles are said to be congruent to each other when they lie in different orientations and positions but remain same in angle measure.
Example:
In here, both \(∠R\) and \(∠Q\) measures \(x°\). Thus, \(∠R\) and \(∠S\) are congruent angles. It can be written as \(∠R\)\(∠Q\)
Congruence of circles
Two circles of the same size (radius, diameter or circumference) are called congruent circles. These circles can also overlap.
Example:
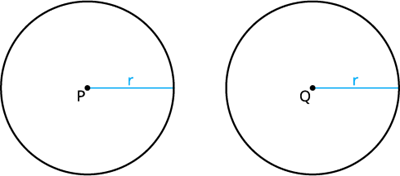
In here, both circles \(P\) and \(Q\) have the same radius of \(r\) units. Thus, circle \(P\) and \(Q\) are congruent circles. These congruent circles can also be denoted as circle \(P\) circle \(Q\)
Congruence of polygons
Two polygons with equal number of sides, all congruent sides, and congruent angles are called congruent polygons.
Example:
In here, the both polygons \(ABCDE\) and \(PQRST\) have \(5\) sides, where \(AB = PQ\), \(BC = QR\), \(CD = RS\), \(DE = ST\) and \(EA = TP\). Also, \(∠A = ∠P\), \(∠B = ∠Q\), \(∠C = ∠R\), \(∠D = ∠S\) and \(∠E = ∠T\), Thus, the polygons \(ABCDE\) and \(PQRST\) have equal number of sides and all the corresponding sides and angles are congruent. So they are congruent polygon. \(ABCDE\) \(PQRST\).
Important!
The notation used to denote congruence between two entities is ''. If the object \(A\) is congruent to object \(B\), it can be denoted as \(A\) \(B\).
Register for free to see more content