PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoConcentric circles:
Two or more circles of the same radii constructed from the same fixed point are called concentric circles.
Circular ring:
The area between two concentric circles is the circular ring.
The width of the circular ring can be obtained by the difference between the radii or diameters of two concentric circles.
\(\text{Width of the circular ring}\) \(=\) \(\text{Outer radii}\) \(-\) \(\text{Inner radii}\)
or
\(\text{Width of the circular ring}\) \(=\) \(\frac{\text{Outer diameter} {-} \text{Inner diameter}}{2}\)
Construction of concentric circles:
Now, let us look at the construction of concentric circles step-by-step.
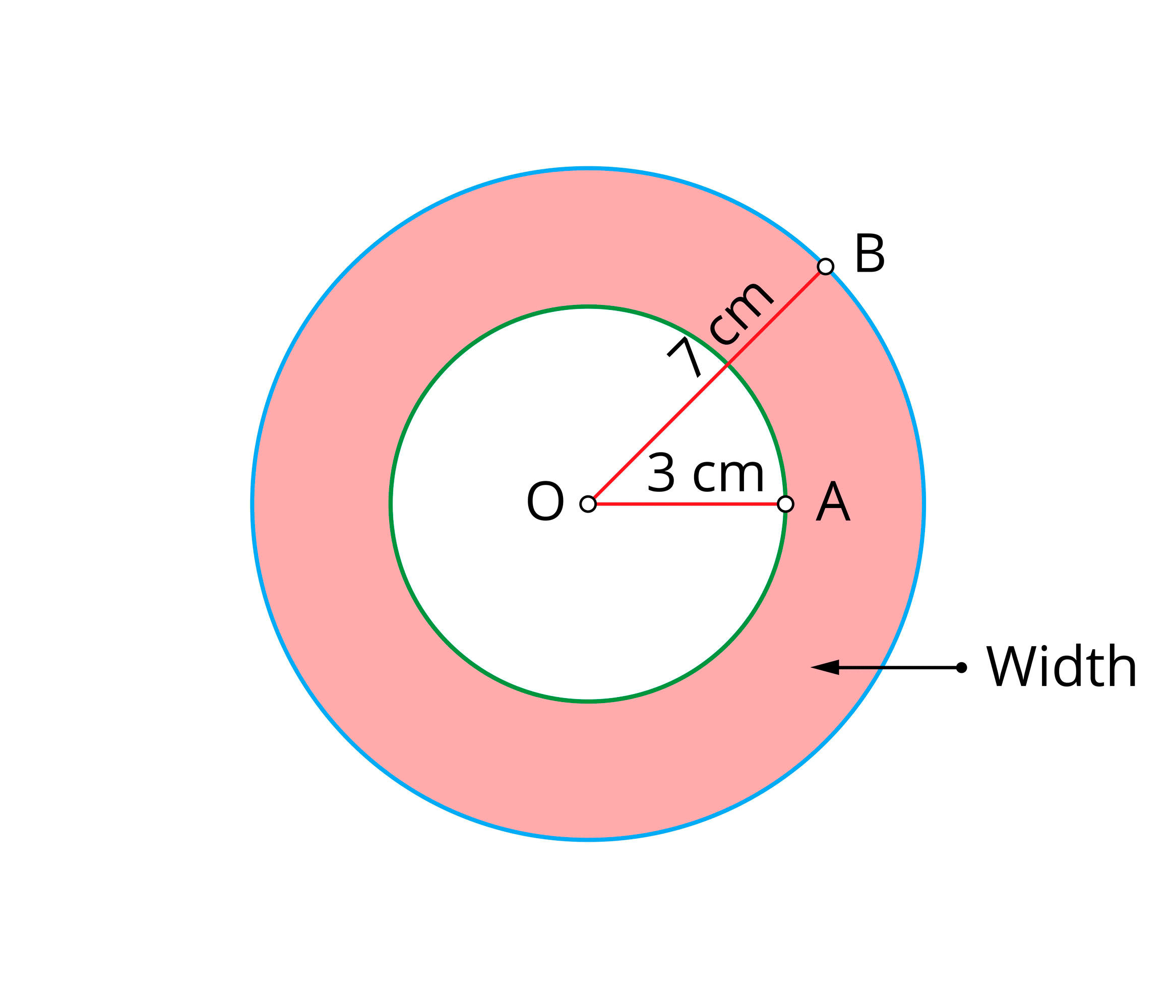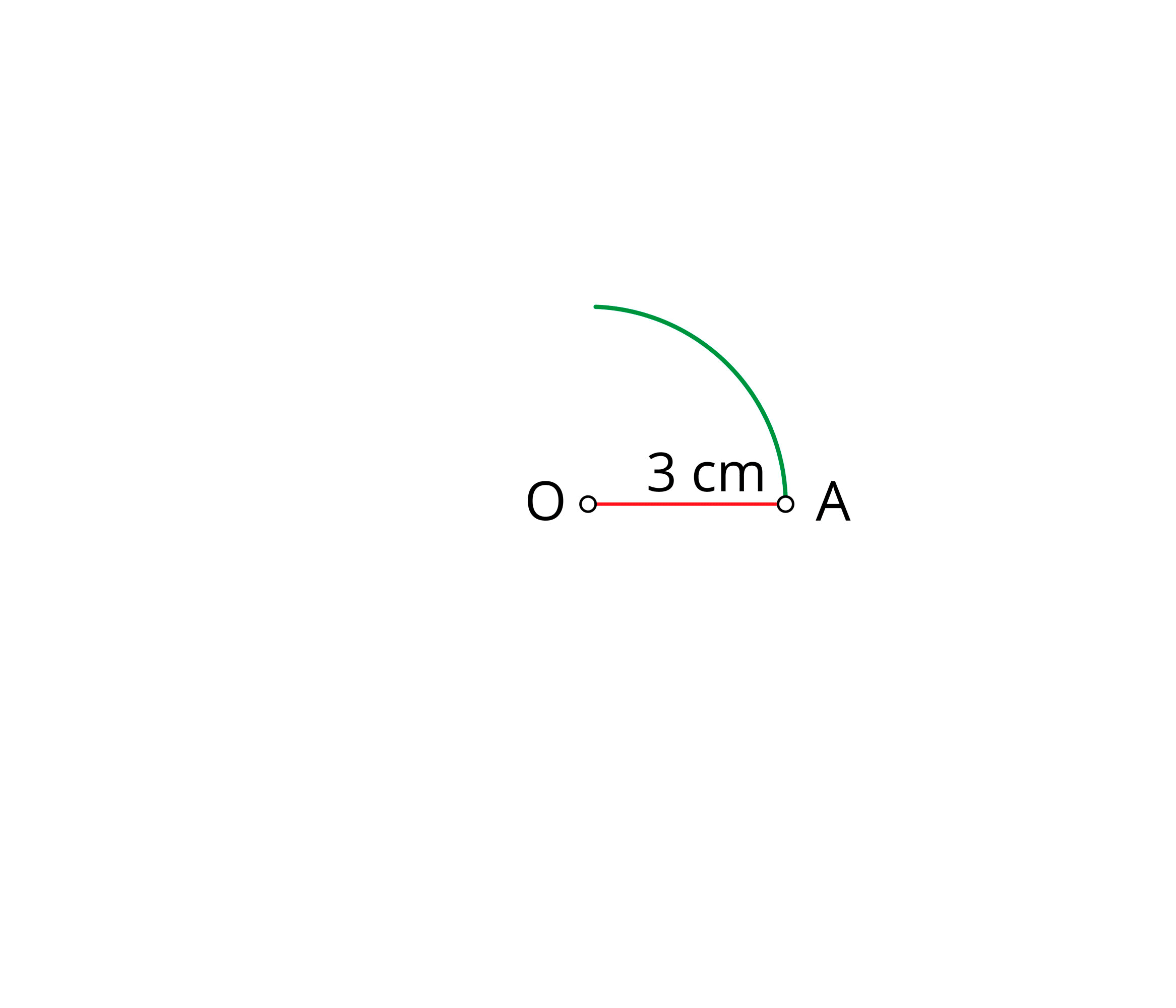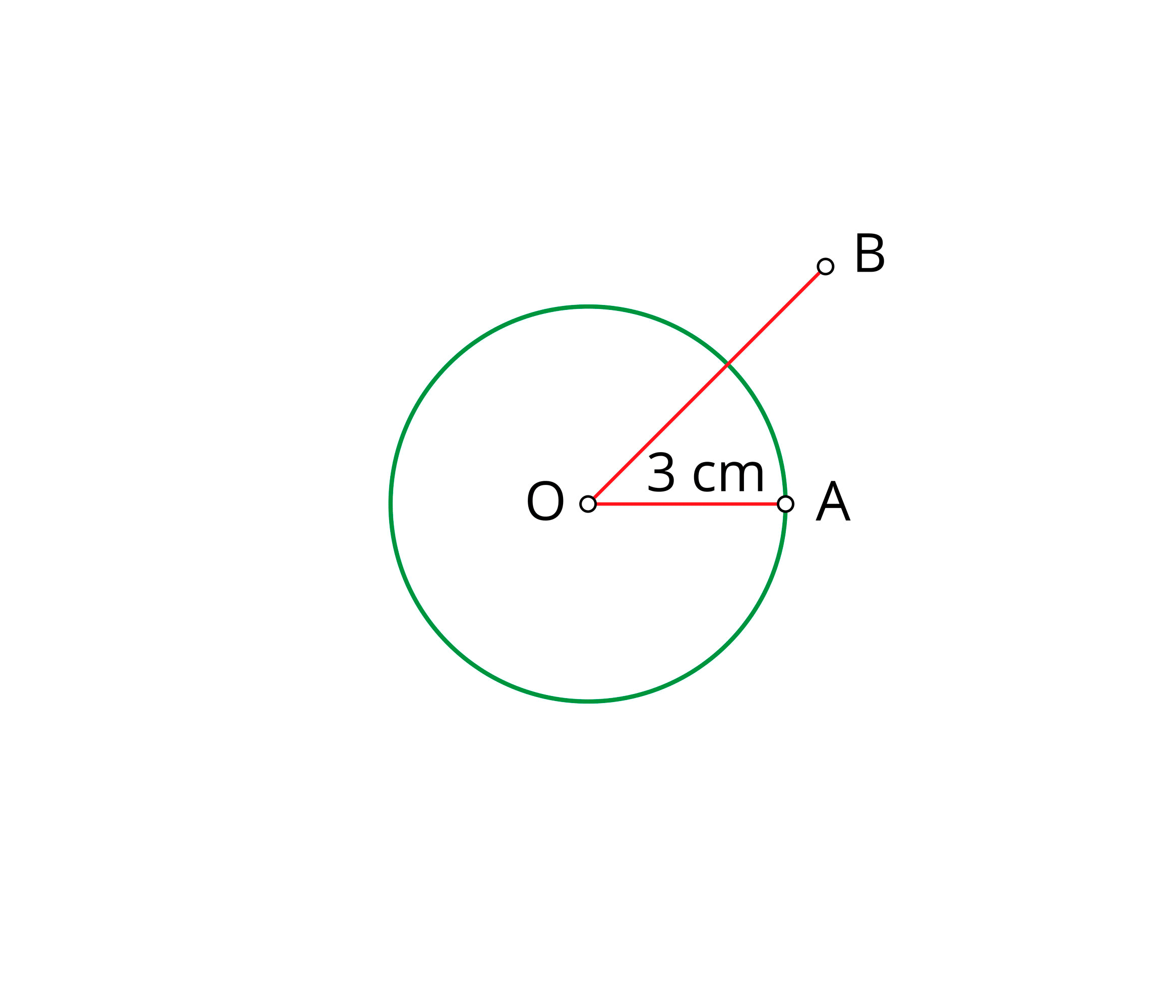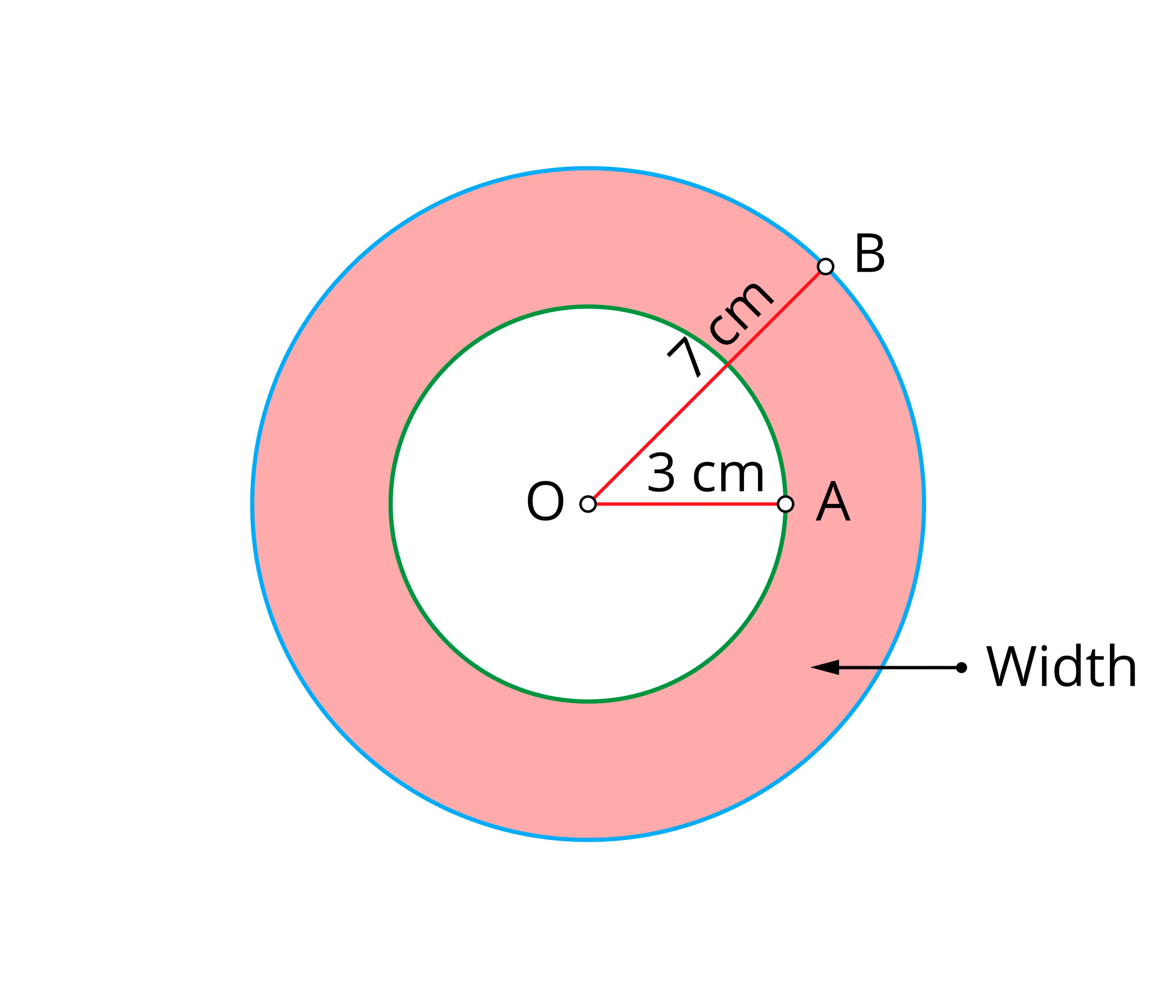
Draw two concentric circles with \(3cm\) and \(7cm\) as radii.
Step \(1\): Draw a rough diagram with the given specifications.
Step \(2\): Mark the fixed point as '\(O\)'.
Step \(3\): Draw a line segment of \(3cm\) from '\(O\)'. Mark the other end of the line segment as '\(A\)'.
Step \(4\): With '\(O\)' as centre, rotate the compass firmly from '\(A\)' until the inner circle is achieved.
Step \(5\): Draw a line segment of \(7cm\) from '\(O\)'. Mark the other end of the line segment as '\(B\)'.
Step \(6\): With '\(O\)' as centre, rotate the compass firmly from '\(B\)' until the outer circle is achieved.
Step \(7\): To find the width of the circular ring.
\(\text{Width of the circular ring}\) \(=\) \(\text{Outer radius}\) \(-\) \(\text{Inner radius}\)
\(=\) \(7\) \(-\) \(3\)
\(=\) \(4\) \(cm\)
The practical construction is as follows:
Register for free to see more content