PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demo1. Two slanting edges of the triangle is always one.
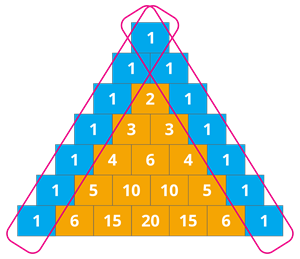
2. First diagonal is counting numbers.
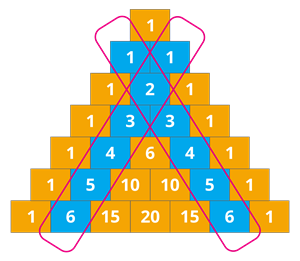
3. The difference between each number on the second diagonal is counting numbers.
From the above triangle, the second diagonal are \(1\), \(3\), \(6\), \(10\) and \(15\).
Difference between the numbers |
\(3 - 1 = 2\) |
\(6 - 3 = 3\) |
\(10 - 6 = 4\) |
\(15 - 6 = 5\) |
The difference between the numbers in the second diagonal is \(2\), \(3\), \(4\) and \(5\). These are counting numbers.
Therefore, the difference between each number on the second diagonal is counting numbers.
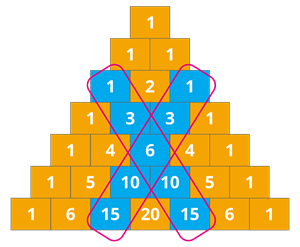
4. The second diagonal numbers are triangular numbers.
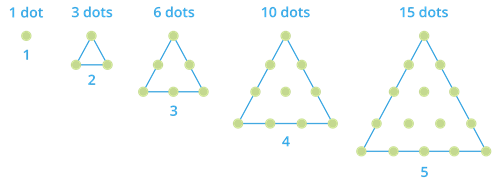
A triangular number is a number that can make an equilateral triangular dot pattern.
For example, \(1\), \(3\), \(6\), \(10\) and \(15\) are triangular numbers.
Therefore, the second diagonal numbers are triangular numbers.
5. Adding the elements in the slanting rows of the Pascal’s Triangle gives Fibonacci sequence.
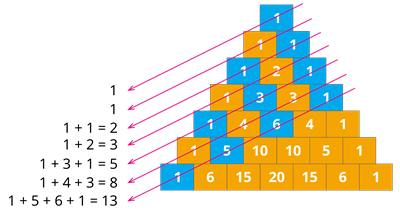
6. Hexagonal pattern:
The product of alternate three numbers in the hexagon is equal to the product of the remaining three alternate numbers.
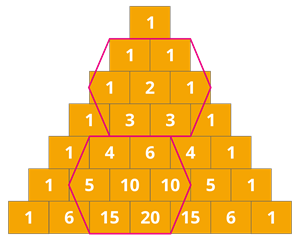
Let's check the given property by taking any two hexagons from the Pascal's triangle.
Hexagonal shape | Product of first three alternate numbers (green colour) | Product of remaining three alternate numbers (blue colour) | Same / Not Same |
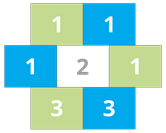 | \(1 \times 1 \times 3 = 3\) | \(1 \times 1 \times 3 = 3\) | Same |
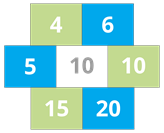 | \(4 \times 10 \times 15 = 600\) | \(6 \times 5 \times 20 = 600\) | Same |
Therefore, the product of alternate three numbers in the hexagon is equal to the product of the remaining three alternate numbers.
Register for free to see more content