PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoTetrominoes, in general, are classified into different types based on the alignment of the four-unit squares present in it. They are orthogonal.
Based on the alignments the tetrominoes are classified into five base types namely,
- Straight-Tetromino
- Square-Tetromino
- \(L\)-Tetromino
- \(Z\)-Tetromino
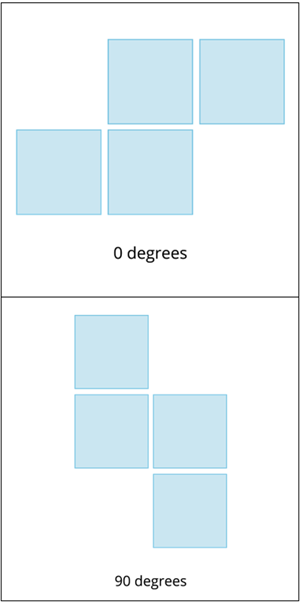
- \(T\)-Tetromino
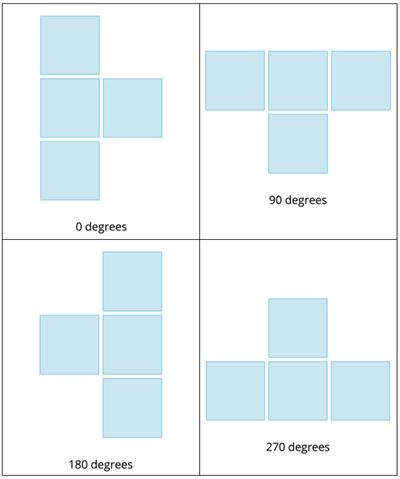
Rotational Properties of Tetrominoes:
- We represent these five tetrominoes in various ways based on their angle of rotation.
- When we rotate the tetrominoes in \(90\) degrees clockwise or anti-clockwise direction, it begins to produce different projections of their base types.
- Even if we rotate tetrominoes to different angles, they remain at their same base type.
- Some tetrominoes exhibit Rotational-Symmetry.
Rotational-Symmetry is the property a shape has when it looks the same after some rotation by a partial turn, and it is the number of distinct orientations in which it seems the same for each rotation.
The different tetrominoes obtained after angular rotations are given below:
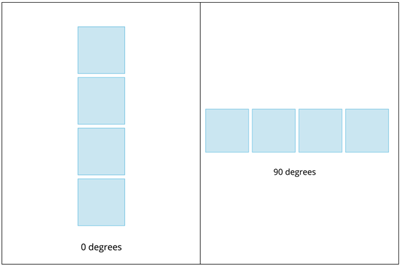
Straight-Tetromino:
- The Straight-Tetromino exhibits \(2\)fold Rotational-Symmetry. That is, the Straight-Tetromino obtains the same shape \(2\) times while undergoing a rotation of \(90\) degrees till it reaches the original shape.
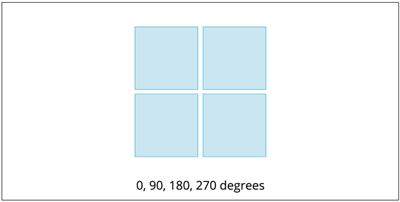
Square-Tetromino:
- The Square-Tetromino exhibits \(4\)fold- Rotational-Symmetry. That is, the Square-Tetromino obtains the same shape \(4\) times while undergoing a rotation of \(90°\) till it reaches the original shape.
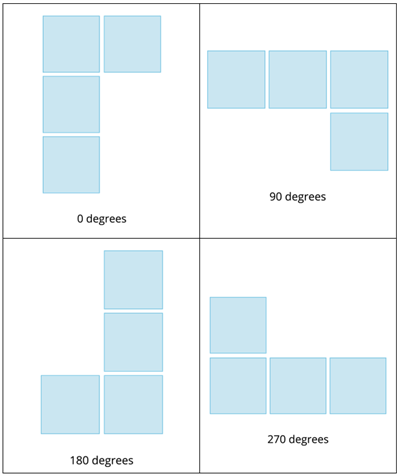
L-Tetromino:
Z-Tetromino:
T-Tetromino:
Register for free to see more content