PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoLet us recall the fundamentals of circles which we studied in previous chapters.
Circle:
A closed line consisting of all points on the plane that are equidistant from a given point on the plane is called a circle.
- The distance across the circle.
- The length of any chord (a straight line which connects two points on a circle) passing through the center.
- It is twice the radius.
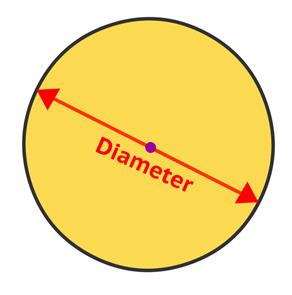
Diameter \(=\) \(2 ×\) Radius \(=\) \(2r\)
Radius of the circle:
The radius is the distance from the center to any point on the circle.
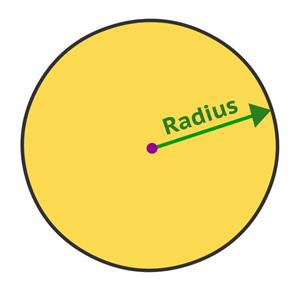
Radius is also known as half of the diameter.
Area of the circle:
The area of a circle is the number of square units inside that circle.
Area of the circle \(=\) sq. units
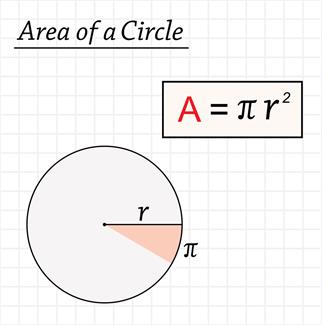
Here \(r\) is the radius of the circle.
The value of the [pi] can be either \(22/7\) or \(3.14\).
Register for free to see more content