PDF chapter test TRY NOW
The fundamental idea about the area of pathways
- We should observe the circular shapes around us to find the area of the pathway.
- The area of the pathway is the difference between the area of the outer circle and the inner circle.
- Let ‘\(R\)’ be the radius of the outer circle, and ‘\(r\)' be the inner circle radius.
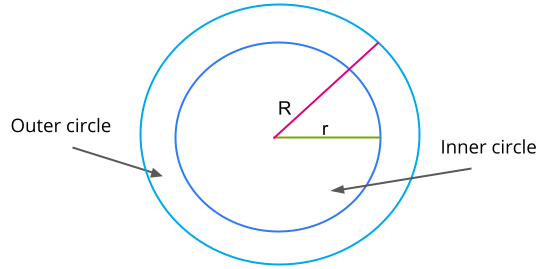
Therefore, we can derive the area of a circular pathway as below.
- The circle is a round plane figure whose boundary (the circumference) consists of points equidistant from the fixed point (the centre).
- Area of the circle is the region enclosed by the circle.
- Distance around the circular region is called the circumference or perimeter of the circle.
Important!
Recollect the formula:
- Area of the circle is .
- Circumference of the circle is .
- Here \(r\) is the radius of the circle.
Register for free to see more content