PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoIn the previous chapter, you learned the fundamental concept of decimal, and it's conversion to fractions.
This chapter discusses how to round off the decimal number and further dive into the arithmetic operation of decimals. Before that, let's recall some basics.
Decimal:
1. A decimal number consists of two parts; a whole number part and a decimal part.
2. These parts are separated by a little dot or point (.) known as a decimal point.
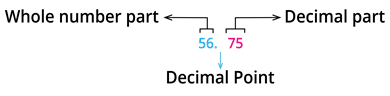
Place value:
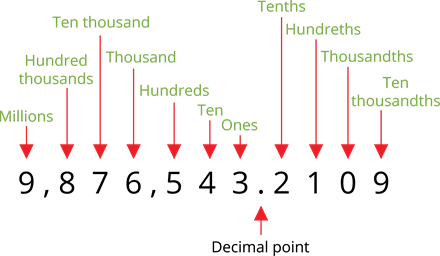
Each digit of a number has a place value. The place value of a digit depends on its position.
Example:
Let us notice the place value of the number \(9\),\(876\),\(543\).\(2109\) below.
Hundredths & tenths place:
- The first digit which placed after a decimal point is called tenths place.
- The tenth place is of the number.
- The second digit which placed after a decimal point is called the hundredth place.
- The hundredth place is .
We can also show decimals using blocks.
Example:
1. Hundreds block have \(100\) boxes.
2. Tens block have \(10\) boxes.
3. Ones block have \(1\) box.
4. Tenths block have boxes of ones block.
5. Hundredths block have boxes of ones block.
In the previous chapter, we studied the general rules for representing decimals on a number line. Here we recall it with an example:
Example:
Locate \(0.5\) on the number line.
Step 1: The decimal number \(0.5\) lies between \(0\) to \(1\).
Step 2: Divide the length between \(0\) to \(1\) into ten equal parts.
Step 3: Move five-step to the right from \(0\).
Step 4: The reached number in number line is \(0.5\).
In the upcoming lessons, we understand how to round off the decimals numbers and practice the same questions.
Register for free to see more content