PDF chapter test TRY NOW
To know clearly about the perpendicular bisectors, we should understand what perpendiculars and bisectors are.
Perpendicular lines:
When two lines or line segments meet at \(90\) degrees, they are called perpendicular lines.
In the figure given above, the \(\overline{AB}\) and \(\overline{MN}\) meet each other at \(90\) degrees at \(R\).
In other words, \(\overline{AR}\) doesn't need to be equal to \(\overline{RB}\).
Bisector:
A line that divides another line into two halves is a bisector.
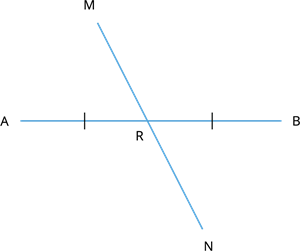
In the figure given above, \(\overline{MN}\) bisects \(\overline{AB}\) at \(R\).
Therefore, \(AR = RB\).
A perpendicular bisector:
A line or a line segment being both perpendicular and acting as a bisector is a perpendicular bisector.
In the figure given above, \(\overline{MN}\) is perpendicular to \(\overline{AB}\), and it also bisects \(\overline{AB}\).
Thus, \(\overline{MN}\) is the perpendicular bisector of \(\overline{AB}\).
Therefore, \(AR = RB\).
Register for free to see more content