UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreA median of a triangle is a line segment joining a vertex to the opposite side's mid-point.
Let us construct a median of a triangle.
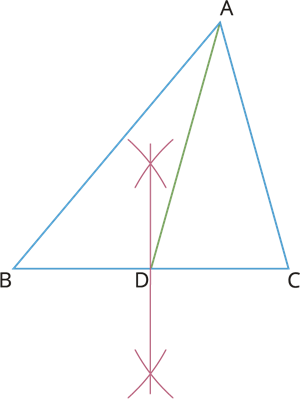
Consider a triangle \(ABC\).
To draw the median, we need to consider any vertex (suppose \(A\)) and its opposite side (\(BC\)).
The midpoint of the side \(BC\) can be found by first constructing the perpendicular bisector (with the help of a compass) on \(BC\) and joining the intersecting arcs.
Let \(D\) be the mid-point of \(BC\).
Now join the point \(D\) and the opposite vertex \(A\). This line segment \(AD\) is the median of a triangle \(ABC\).
Important!
1. As there are three vertices for any triangle, every triangle has three medians, one from each vertex.
2. Thus, a median connects a vertex of a triangle to the opposite side's mid-point.
3. The medians of the triangle are concurrent as they intersect at only one point.
4. A median from the vertex divides the opposite side into two equal parts. That is, a median from any vertex meets the opposite side's mid-point.
Register for free to see more content