UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreVisual Illustration:
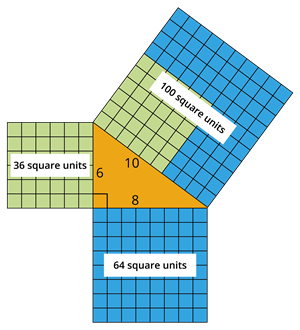
This visual representation will help you understand the Pythagorean theorem better.
In the given figure, the right angled triangle formed by the sides of the squares of dimensions \(6\) units, \(8\) units and \(10\) units.
Here the sides with measure \(6\) units and \(8\) units form the sides or legs of the triangle, whereas the side with measure \(10\) units form the hypotenuse as the longest side of the right triangle is called the hypotenuse.
From the figure, it is observed that:
The area of the square with side \(6\) units \(=\) \(6 \times 6\)
\(=\) \(36\) square units
The area of the square with side \(8\) units \(=\) \(8 \times 8\)
\(=\) \(64\) square units
The area of the square with side \(10\) units \(=\) \(10 \times 10\)
\(=\) \(100\) square units
Here, \(100\) square units \(=\) \(36\) square units \(+\) \(64\) square units.
That is, \(10^2\) \(=\) \(6^2\) \(+\) \(8^2\).
The above equation represents the theorem from the figure that the number of units square on the hypotenuse is equal to the sum of the unit squares on the other two sides.
Important!
Click here! to recall what is a right triangle and the terms used in a right triangle.
The converse of the theorem:
If in a triangle, the square on the greatest side is equal to the sum of squares on the other two sides, then the triangle is a right angled triangle.
Explanation:
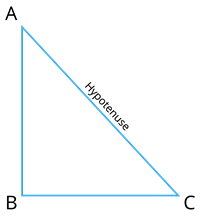
In the triangle \(ABC\), if \(AC^2 = AB^2 + BC^2\) then, the triangle is a right angled triangle where \(\angle B = 90^{\circ}\).
Example:
In the above given visual, consider the triangle with measures \(6\) units, \(8\) units and \(10\) units.
Here, the length of the hypotenuse is \(10\) units, and the length of the other two sides are \(6\) units and \(8\) units.
Let us verify whether the triangle with these dimensions is right angled.
Square of the hypotenuse \(=\) \(10^2\)
\(=\) \(100\)
Sum of squares on the other two sides\(=\) \(6^2\) \(+\) \(8^2\)
\(=\) \(36 + 64\)
\(=\) \(100\)
Here, the square on the hypotenuse is equal to the sum of squares on the other two sides.
Therefore, by the converse of the theorem, the triangle is a right angled triangle.
Important!
(i) The three positive integers \(x\), \(y\) and \(z\) which satisfies the Pythagorean theorem are called Pythagorean triplets.
Example:
(ii) If \(l\) is any positive integer and \((x, y, z)\) is a Pythagorean triplet, then \((lx, ly, kz)\) is also a Pythagorean triplet.