PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoWorking rule to construct a parallelogram:
Let us discuss the working rule to construct a parallelogram when the measure of one side, one angle and one diagonal of a parallelogram are given.
Example:
Construct a parallelogram \(JUMP\) with \(JU\) \(=\) \(8.5\) \(cm\), \(JM\) \(=\) \(9\) \(cm\) and \(\angle JUM\) \(=\) \(75^{\circ}\). Also, find its area.
Construction:
Step 1: Draw a line segment \(JU\) \(=\) \(8.5\) \(cm\).
Step 2: With \(U\) as centre, mark an angle \(75^{\circ}\) using a protractor and mark it as \(X\). Join \(QX\).
Step 3: With \(J\) as centre, draw an arc of radius \(9\) \(cm\) intersecting \(QX\) at \(M\). Join \(JU\).
Step 4: Measure \(UM\), and with \(J\) as centre, draw an arc of radius that is equal to the measure of \(UM\).
Step 5: With \(M\) as centre, draw an arc of radius \(8.5\) \(cm\) intersecting the previous arc at \(P\).
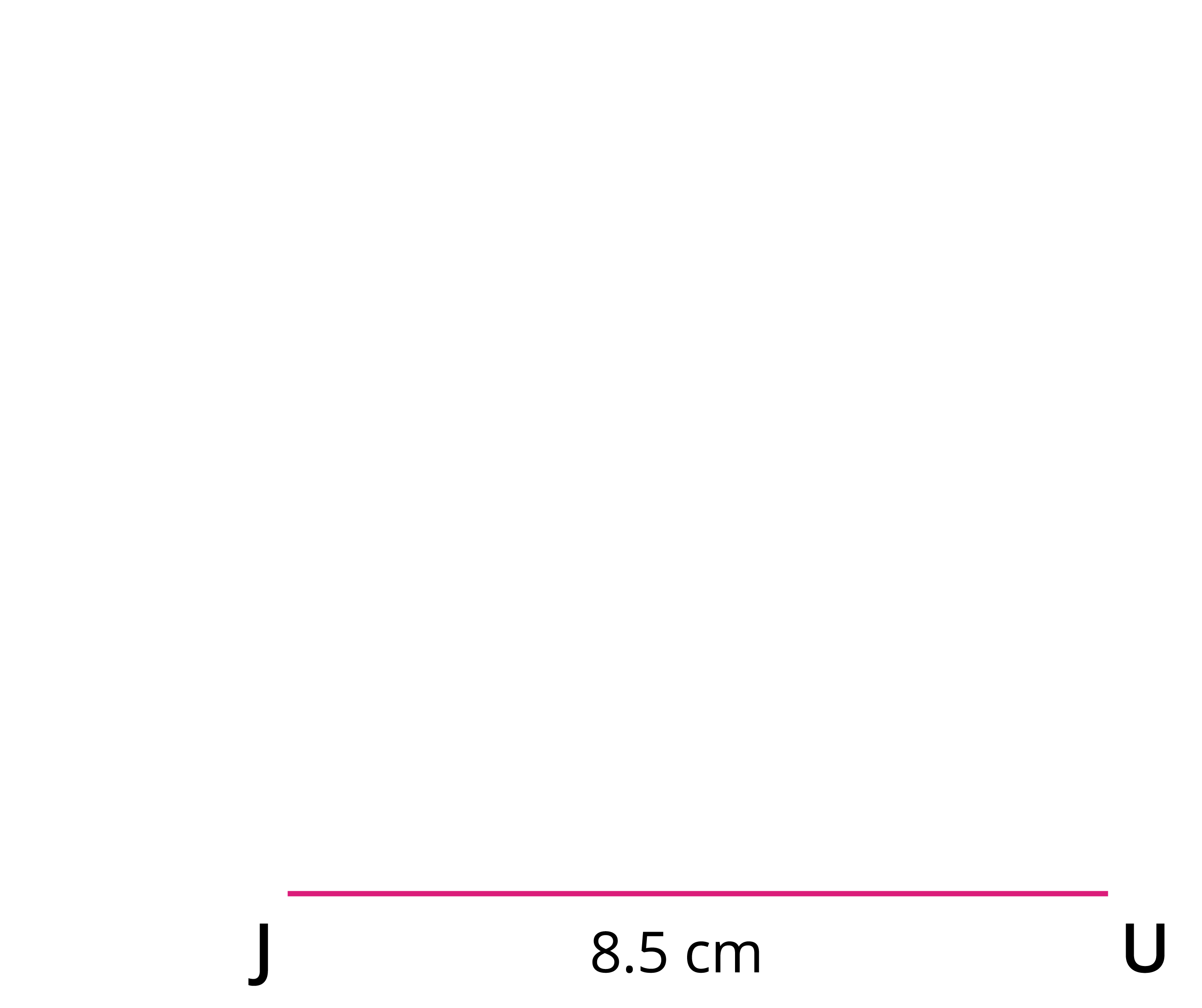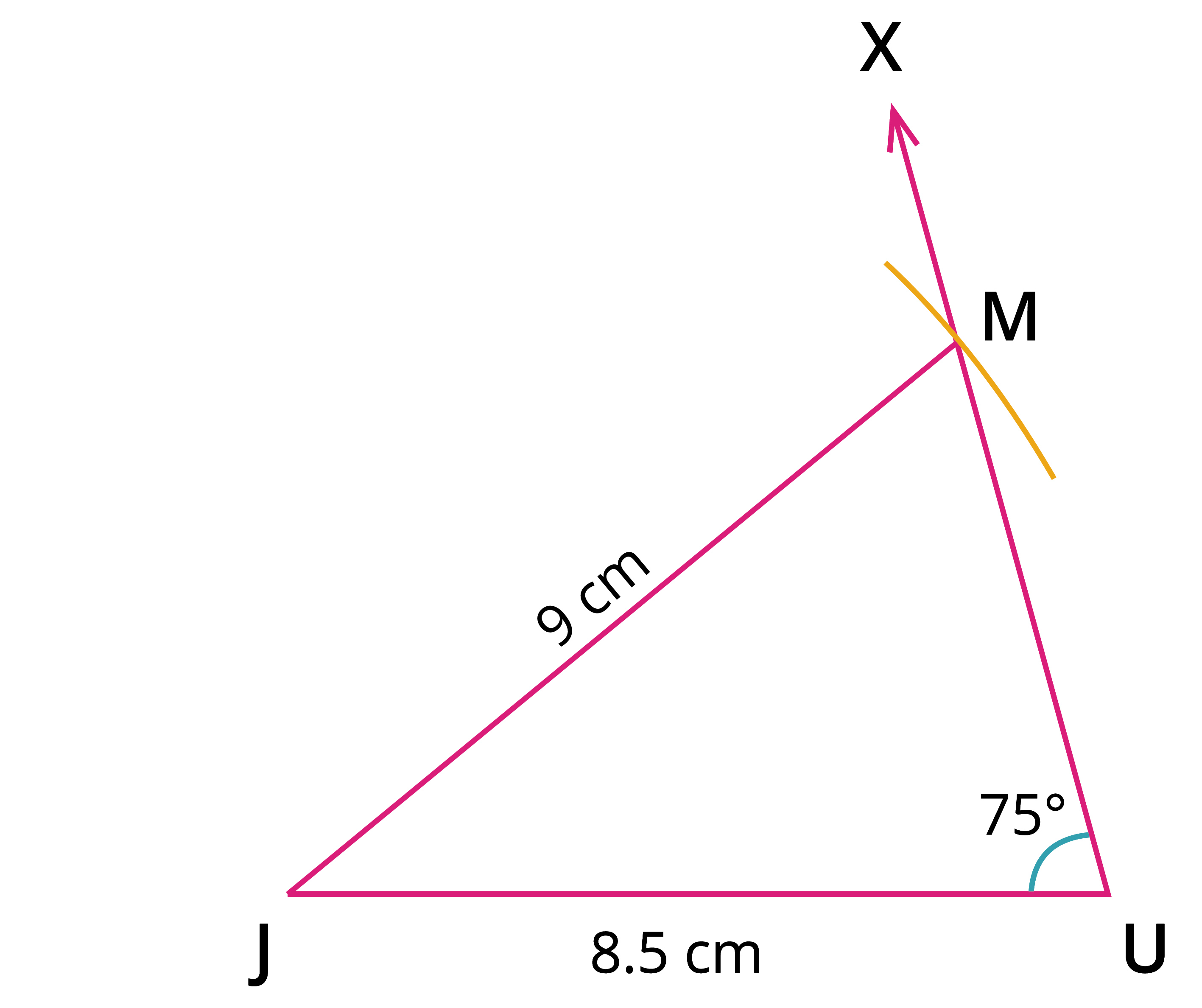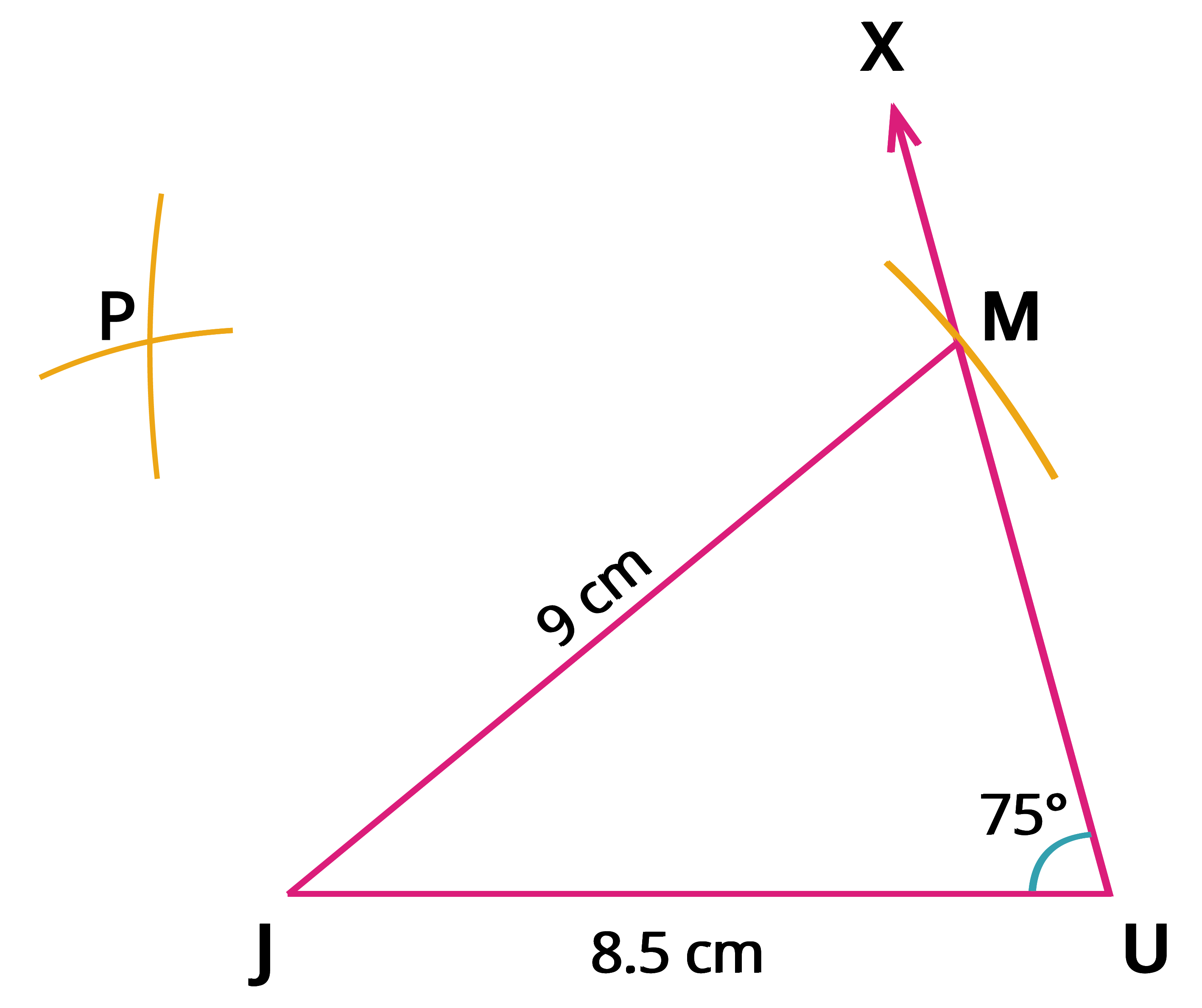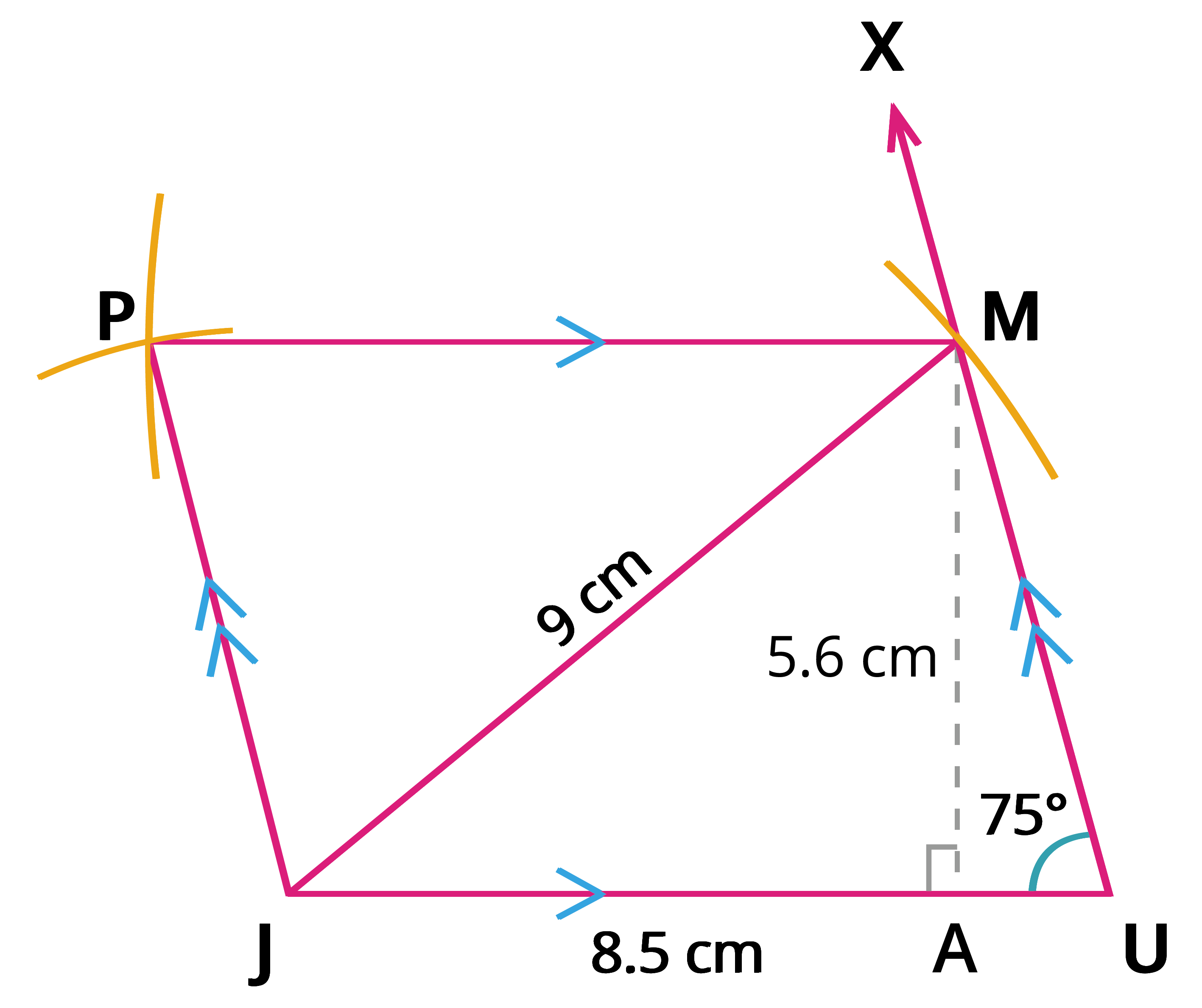
Step 6: Join \(MP\) and \(MJ\).
Step 7: \(JUMP\) is the required parallelogram. The measure of \(MA\) gives the height of the parallelogram \(JUMP\).
Area calculation:
Area of the parallelogram \(=\) \(base \times height\) square units
\(=\) \(8.5 \times 5.6\)
\(=\) \(47.60\) \(cm^2\)
Register for free to see more content