PDF chapter test TRY NOW
Working rule to construct a trapezium:
Let us discuss the working rule to construct a trapezium when the measure of all the four sides of a trapezium are given.
Example:
Construct a trapezium \(ABCD\) in which \(\overline{AB}\) is parallel to \(\overline{CD}\), \(AB\) \(=\) \(9\) \(cm\), \(BC\) \(=\) \(5\) \(cm\), \(CD\) \(=\) \(6\) \(cm\) and \(DA\) \(=\) \(6.5\) \(cm\). Also, find its area.
Construction:
Step 1: Draw a line segment \(AB\) \(=\) \(9\) \(cm\).
Step 2: Mark a point \(P\) on the line segment \(AB\) such that \(AP\) \(=\) \(6cm\).
Step 3: With \(P\) and \(B\) as centres, draw two arcs of radii \(6.5\) \(cm\) and \(5\) \(cm\) respectively such that they intersect each other at \(C\).
Step 4: Join \(PC\) and \(BC\).
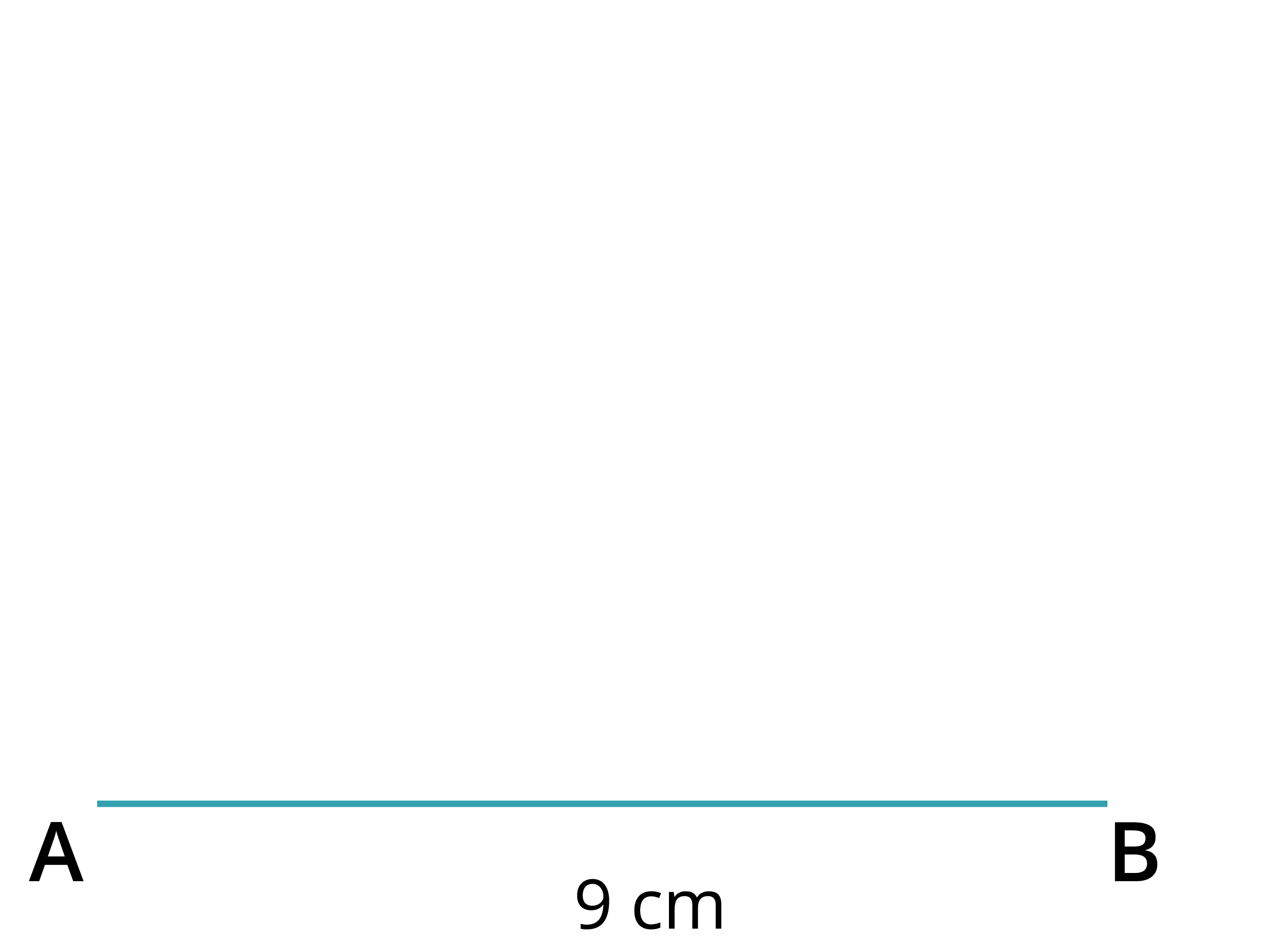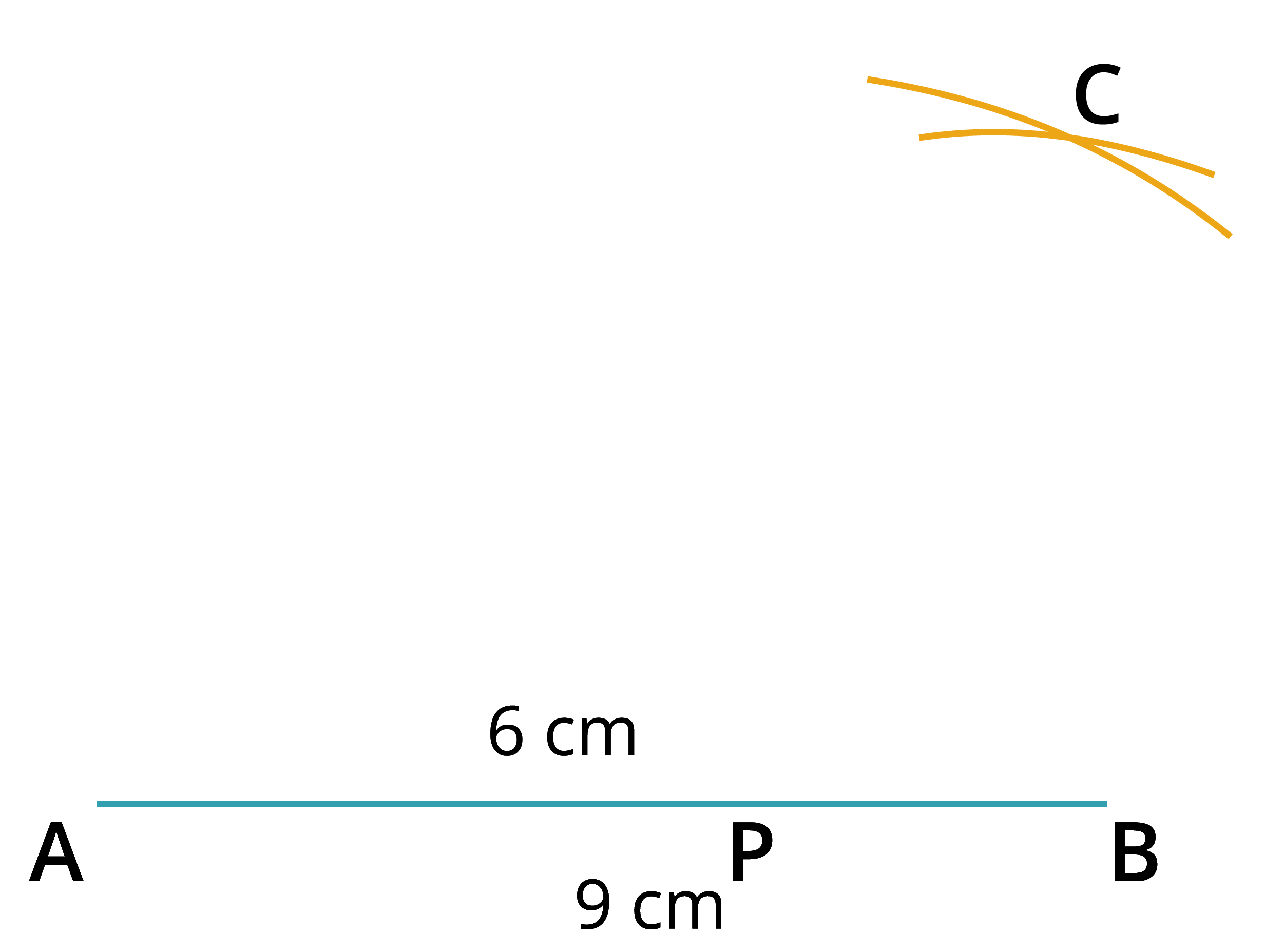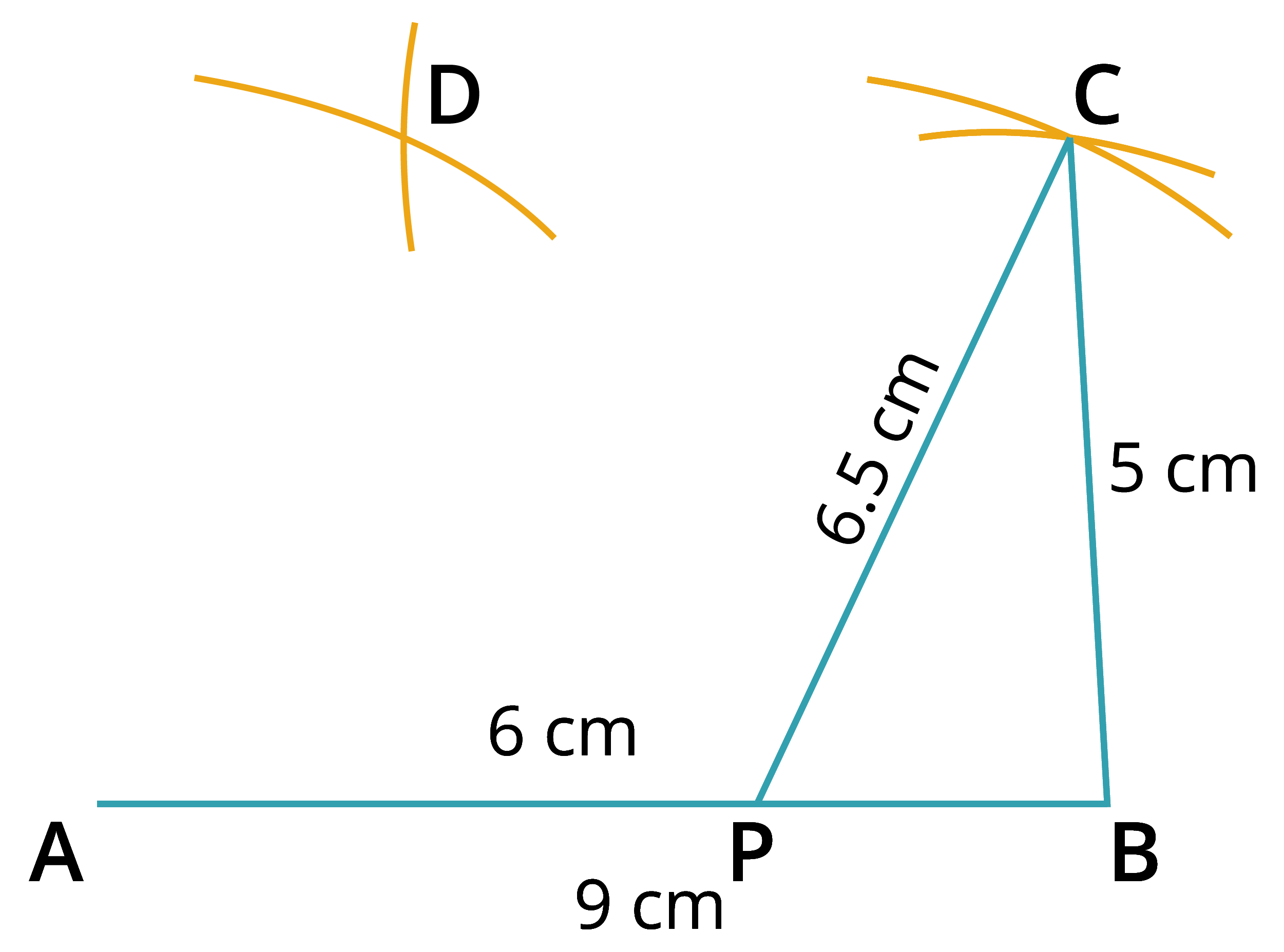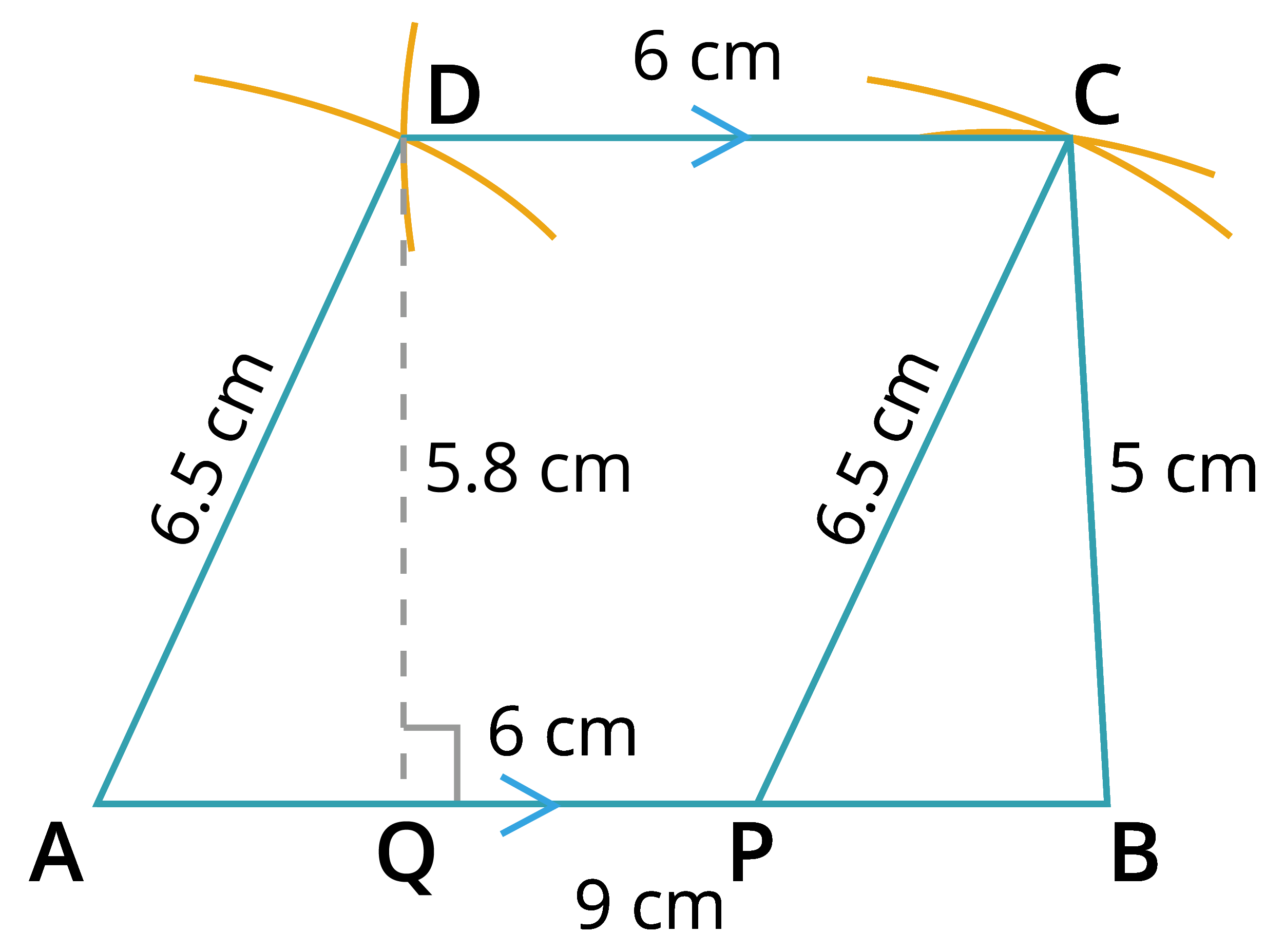
Step 5: With \(C\) and \(A\) as centres, draw two arcs of radii \(6\) \(cm\) and \(6.5\) \(cm\) respectively such that they intersect each other at \(D\).
Step 6: Join \(AD\) and \(CD\).
Step 7: \(ABCD\) is the required trapezium. The measure of \(DQ\) gives the height of the trapezium \(ABCD\).
Area calculation:
Area of the trapezium \(ABCD\) \(=\) \(\frac{1}{2} \times h \times (a + b)\) square units
\(=\) \(\frac{1}{2} \times 5.8 \times (9 + 6)\)
\(=\) \(\frac{1}{2} \times 5.8 \times 15\)
\(=\) \(\frac{87}{2}\)
\(=\) \(43.50\) \(cm^2\)
Register for free to see more content