UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreTrapezium:
A trapezium is a quadrilateral (four-sided figure) in which a pair of opposite sides are parallel and a pair of opposite sides are not parallel.
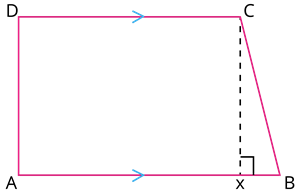
In the figure, the sides \(AB\) and \(CD\) are parallel, and \(AD\) and \(BC\) are non-parallel.
Important!
• The distance between the parallel sides of a trapezium is called the height. In the figure, \(CX\) is the height.
• Sum of all the angles in a trapezium is \(360^{\circ}\).
Isosceles trapezium:
If the non-parallel sides of a trapezium are equal in length and form equal angles at one of its bases, then it is called an isosceles trapezium.
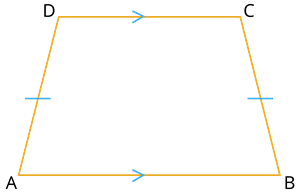
In the figure, the non-parallel sides \(AD\) and \(BC\) are equal, and \(\angle A\) and \(\angle B\) are equal.
Area of the trapezium:
The area of any trapezium is calculated using the formula \(A = \frac{1}{2} \times h \times (a +b)\) square units.
Where \(h\) represents the height of the trapezium.
\(a\) and \(b\) are the lengths of the parallel sides.
Example:
If the height of the trapezium is \(12\) \(cm\) and the lengths of the parallel sides are \(5\) \(cm\) and \(6\) \(cm\) respectively then find its area.
Solution:
Given \(h\) \(=\) \(12\) \(cm\), \(a\) \(=\) \(5\) \(cm\) and \(b\) \(=\) \(6\) \(cm\).
Area of the trapezium, \(A\) \(=\) \(\frac{1}{2} \times h \times (a +b)\)
\(=\) \(\frac{1}{2} \times 12 \times (5 + 6)\)
\(=\) \(6 \times 11\)
\(=\) \(66\) \(cm^2\)
Ways to construct a trapezium:
A trapezium can be constructed if one of the following four measurements are given.
(i) Three sides and one diagonal.
(ii) Three sides and one angle.
(iii) Two sides and two angles.
(iv) Four sides.
Register for free to see more content