UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreLet us see the types of cipher codes:
1. Shifting Cypher text:
If you want to send a message anonymously, you should encrypt it (translate it into a hidden code). A shift cypher is one of the easiest ways to do this.
In history, many Kings have used this kind of cypher while communicating with their military commanders.
In history, many Kings have used this kind of cypher while communicating with their military commanders.
In a shift cypher, each letter in the message is replaced by a letter in a specific set number of positions along with the alphabet.
That particular number position is known as the encryption key, which is nothing but the length of the shift we are using.
Example:
Plain text to ciphertext or Encoding:
We can encrypt a word "mathematics" using a shift cipher with encryption key \(+2\).
Since, the key \(+2\), the letters are shifted two places forward. That is \(a\) becomes \(c\), \(b\) becomes \(d\), and \(c\) becomes \(e\).
Conversion of plain text to ciphertext when the key \(+2\):
Plain text | Ciphertext |
\(m\) | \(O\) |
\(a\) | \(C\) |
\(t\) | \(V\) |
\(h\) | \(J\) |
\(e\) | \(G\) |
\(m\) | \(O\) |
\(a\) | \(C\) |
\(t\) | \(V\) |
\(i\) | \(K\) |
\(c\) | \(E\) |
\(s\) | \(U\) |
Therefore, using the key \(+2\) we can encode message as (or ciphertext): "OCVJGOCVKEU".
Ciphertext to Plain text or Decoding:
Let us see the how we can decode the cipher text "L ORYH PDWKHPDWLFV" with a key \(+3\).
Since, the key is \(+3\), the plain text has been shifted \(4\) places forward. So, decode the code we have to inverse the cipher text to \(3\) letters. Then the new key will be \(-3\).
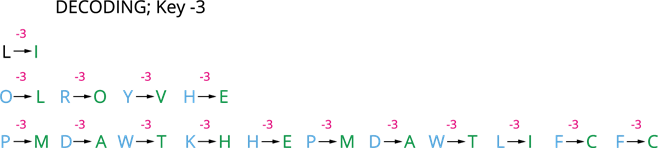
2. Substituting Cypher text
In substituting cypher text, each letters in the plain text is “substituted” by the certain letters, numbers and symbols.
Example:
Alpha-substitution:
Let's take the words "orange", "apple" as plain text and we convert it as cipher text by Substituting the certain alphabets to each letters.
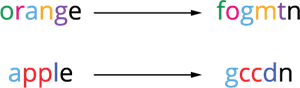
Observe the above encrypted codes. Each of the letters corresponds to the specific letters. All the words are substituted as the particular words. Such, that the letter "\(a\)" is substituted as "\(g\)", the letter "\(e\)" is substituted as "\(n\)".
Using the same pattern, now we encode the word "grape" as "togcn"
Alpha-numeric substitution:
First observe the below figure which explains the alphanumeric relation, in terms of place value.
When key \(= 1\)
Let's code the word "orange" using place value of each letters.
orange \(=\) \(15\) \(18\) \(1\) \(14\) \(7\) \(5\)
apple \(=\) \(1\) \(16\) \(16\) \(9\) \(5\)
Now, try to decode the cypher text \(10\) \(1\) \(13\) \(5\) \(19\)?
Answer: The decrypted code of \(10\) \(1\) \(13\) \(5\) \(19\) is JAMES.
We should keep it in mind that when the key is \(1\), then only \(a=1\), \(b=2\), but when the key changes to \(2\), \(3\) or some number the substitution of the number to the letter should vary as well.
Register for free to see more content