PDF chapter test TRY NOW
In Mathematics, the objective of the 'Map colouring' is to find the minimum number of colours to paint the map. This way of logical thinking helps us to think about what we should do when the available resources are minimal to solve the task or problems. This thought process can help us a lot in our daily life.
Map colouring is a simple act of painting the map on its different features by applying different colours.
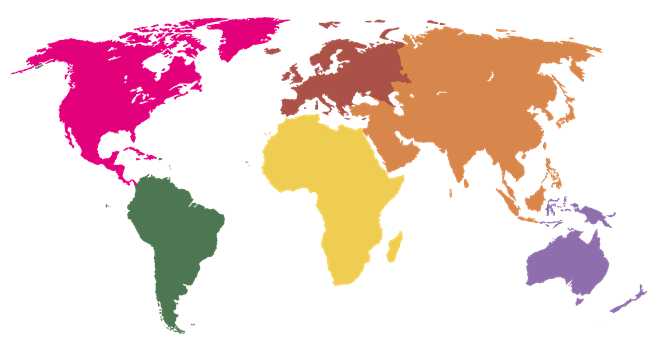
Now observe the below map of our Continents. We can notice that each continent is coloured with different colours. So the maximum colours required to paint the map is equal to the number of regions in the maps.
Map colouring is a simple act of painting the map on its different features by applying different colours.
Now observe the below map of our Continents. We can notice that each continent is coloured with different colours. So the maximum colours required to paint the map is equal to the number of regions in the maps.
But how do you find the minimum number of colours required so that no adjacent regions have the same colours?
The answer is so simple. If we figure out the vertices of the map, then we can easily assign the individual colours so that no adjacent regions have the same colours.
The answer is so simple. If we figure out the vertices of the map, then we can easily assign the individual colours so that no adjacent regions have the same colours.
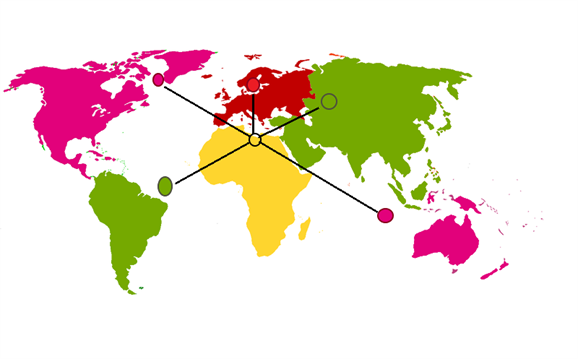
In the above figure, we can notice that there minimum \(4\) colours are used, and to avoid the same colours in adjacent sides, the opposite regions are coloured as same.
