PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoA polyhedron is a three-dimensional shape with flat polygonal faces, straight edges and sharp vertices. In other words, the \(3D\) solids with flat surfaces are called polyhedrons.
There are two types of polyhedrons.
1. Convex polyhedron
2. Concave polyhedron
A polyhedron whose surface(faces, edges and vertices) does not intersect is referred to as a convex polyhedron.
A polyhedron the surface of which intersects is called a concave polyhedron.
Some special types:
A non-polyhedron is a three-dimensional, curved-faced shape.
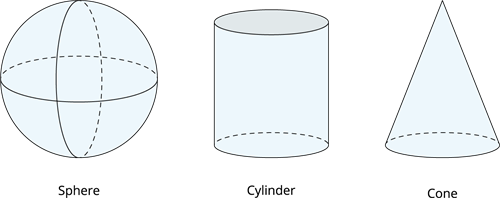
A polyhedron is said to be regular if its faces consist of regular polygons and meet on each vertex with the same number of faces.
There are five regular polyhedrons in it:
- A regular polyhedron which is made up of six square is called a cube. It consists of \(6\) square faces, \(12\) edges and \(8\) vertex corners.
- A triangular pyramid, also known as a tetrahedron. It consists of \(4\) equilateral triangular faces, \(6\) straight edges, and \(4\) vertex corners.
- A regular polygon which is made up of eight equilateral triangles is called octahedron. It consists of \(8\) equilateral triangular faces, \(12\) edges, and \(6\) vertex corners.
- A regular polygon which is made up of twelve flat faces of pentagons is called a dodecahedron. It consists of \(12\) pentagon faces, \(30\) edges, and \(20\) vertex corners.
- A regular polygon which is made up of twenty equilateral triangles is called an icosahedron. It consists of \(20\) equilateral triangular faces, \(30\) edges, and \(12\) vertex corners.
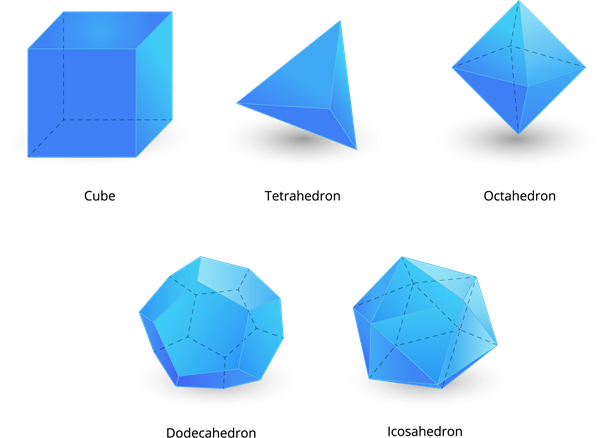
These five convex regular polyhedrons are called platonic solids.
Euler Formula: For any convex polyhedrons, .
Where '\(F\)' is the number of faces, '\(V\)' the number of vertices and '\(E\)' is the number of edges.
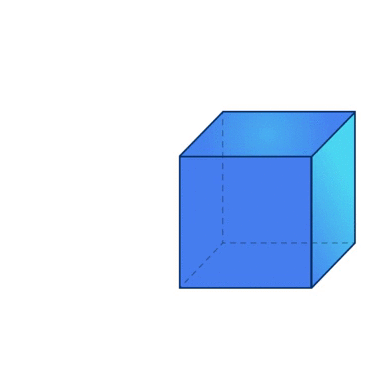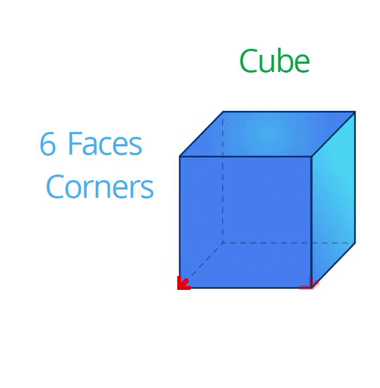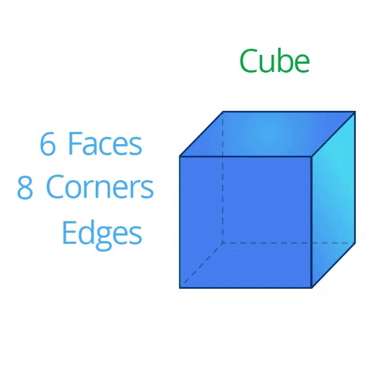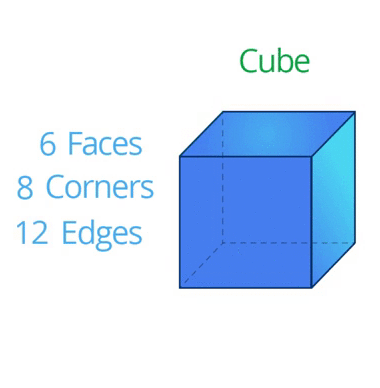
We know that the cube has \(6\) faces, \(8\) corners, and \(12\) edges.
Now, we substitute all the values in the Euler's formula.
Important!
1. Sometimes adding an edge between two non-adjacent vertices will not affect Euler formula.
Example:
2. Euler formula does not work if the shape has any holes and if the shape is made up of two pieces stuck together(by a vertex or an edge).
Example:
Register for free to see more content