PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

Book Free Demo

9. Area and its perimeter of a parallelogram

To calculate the area of a parallelogram, multiply the base times '

$b$ ' the height '

$h$ '.

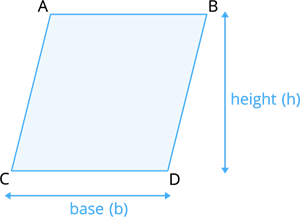
Area of parallelogram

$A =$

$b × h$

$square$

$units$ .

Example:

A parallelogram has a base of

$6 m$ and

$3 m$ height, what is its area?

Let the base

$b= 6m$ and the height

$h= 3m$ .

Area

$A = b × h = 6m × 3m =18m²$ .

To calculate the base of the parallelogram, divide area '

$A$ ' by height '

$h$ '.

Base of parallelogram

$b = A/h$ unit.

Example:

A parallelogram has an area of

$64 m²$ and its height

$4 m$ , what is its base?

Let the area

$A= 64m²$ and the height

$h= 4m$ .

Base

$=$

$\frac{A}{h} = \frac{64}{4} = 16 m$ .

To calculate the height of the parallelogram, divide area '

$A$ ' by base '

$b$ '.

Height of parallelogram

$h = A/b$ unit.

Example:

A parallelogram has an area of

$64 m²$ and

$16 m$ base, what is its height?

Let the area

$A= 64m²$ and the height

$h= 16m$ .

Height

$=$

$\frac{A}{b} = \frac{64}{16} = 4 m$ .

Where '

$A$ ' is denoted as area, '

$b$ ' is denoted as the base and '

$h$ ' is denoted as the height.

To calculate the perimeter of a parallelogram, multiply

$2$ times the (base

$+$ side length).

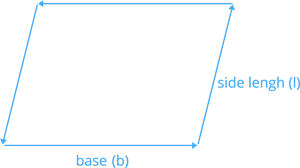
Perimeter of parallelogram

$P = 2 (b + l)$ .

Where '

$b$ ' is denoted as the base, and '

$l$ ' is denoted as the side length.

Example:

A parallelogram has a base of

$5 m$ and

$3 m$ length, what is its perimeter?

Here the base

$b= 5m$ and the side length

$l= 3m$ .

Perimeter

$=2(b + l)$

$=2(5+3)$

$=2(8)$

$=16m$ .

Previous theory

Exit to the topic

Next theory

Send feedback

Did you find an error?

Send it to us!

9. Area and its perimeter of a parallelogram

Theory: