
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoWhat are simultaneous linear equations?
A set of equations with two or more linear equations having the same variables is called as simultaneous linear equations or system of linear equations or a pair of linear equations.
\(2x+y=1\) and \(x-y=3\)
Together they are called as simultaneous linear equations.
Example:
Jane bought \(2\) apples and \(1\) banana for a total cost of \($8\). Let us frame an equation to find the individual cost of an apple and a banana.
Let us understand the purpose of simultaneous linear equations with a real life situation.
Let \(x\) denote the cost of an apple and \(y\) denote the cost of a banana.
Writing in equation, she has:
\(2x+y=8\) ---- \((1)\)
Jane tries to find the value of each apple and banana by substituting the values for \(x\).
When \(x=1\), \(2(1)+y=8\)\(\Rightarrow y=8-2\)\(\Rightarrow y=6\)
When \(x=2\), \(2(2)+y=8\)\(\Rightarrow y=8-4\)\(\Rightarrow y=4\)
When \(x=3\), \(2(3)+y=8\)\(\Rightarrow y=8-6\)\(\Rightarrow y=2\)
When \(x=4\), \(2(4)+y=8\)\(\Rightarrow y=8-8\)\(\Rightarrow y=0\)
Now, writing these values in the table, we have:
\(x\) | \(1\) | \(2\) | \(3\) | \(4\) | …. |
| \(y\) | \(6\) | \(4\) | \(2\) | \(0\) | …. |
Jane plots these points in the graph and draws a line joining these points.
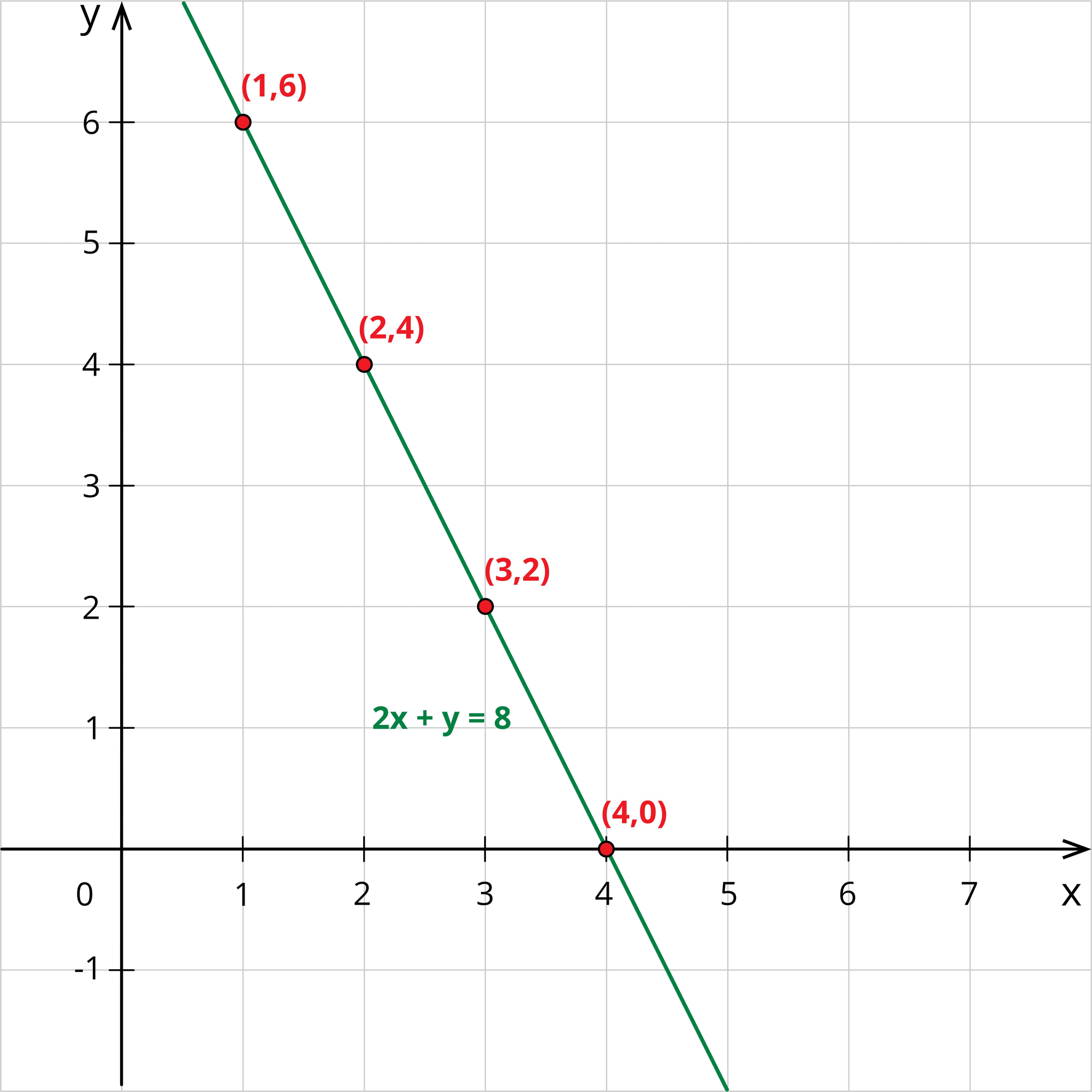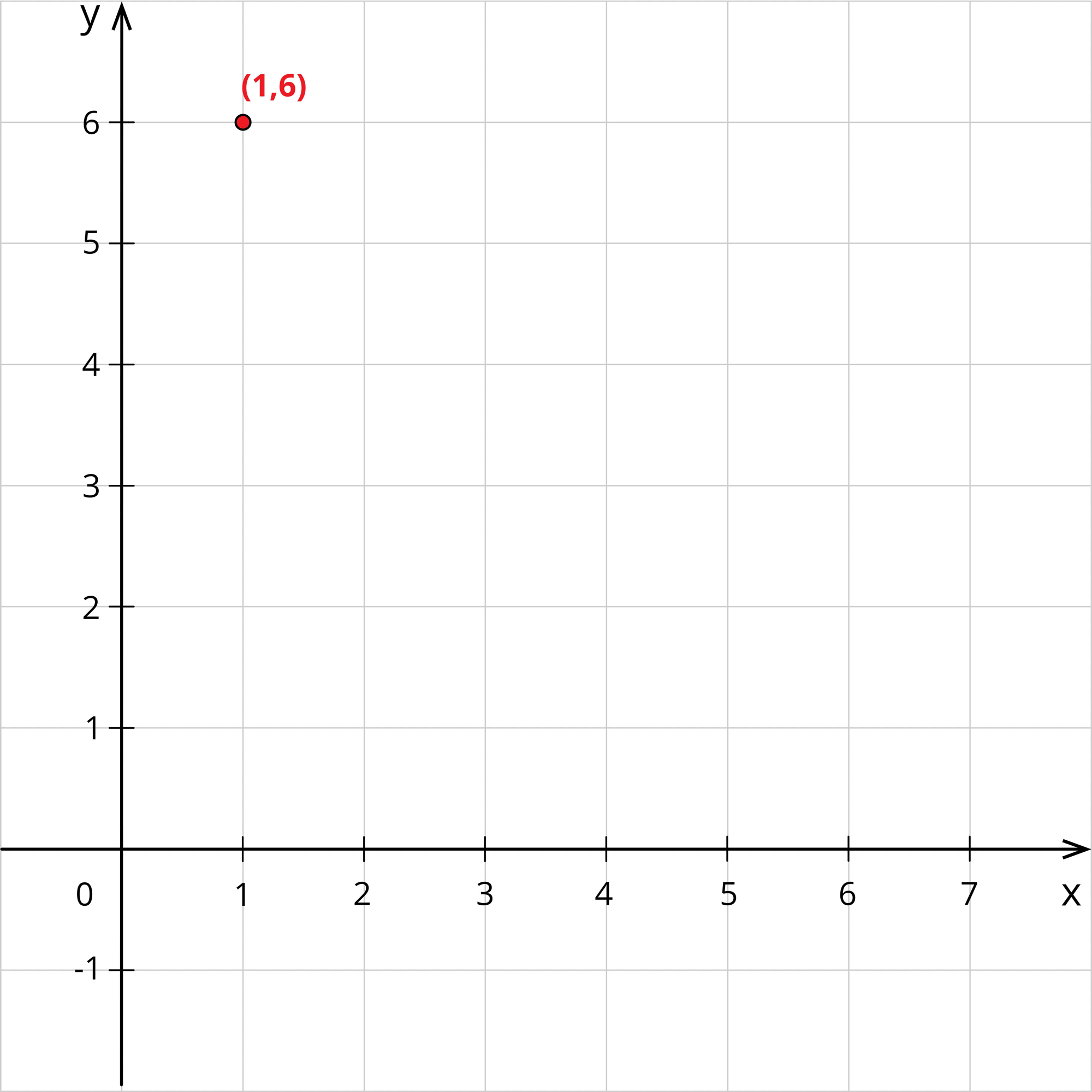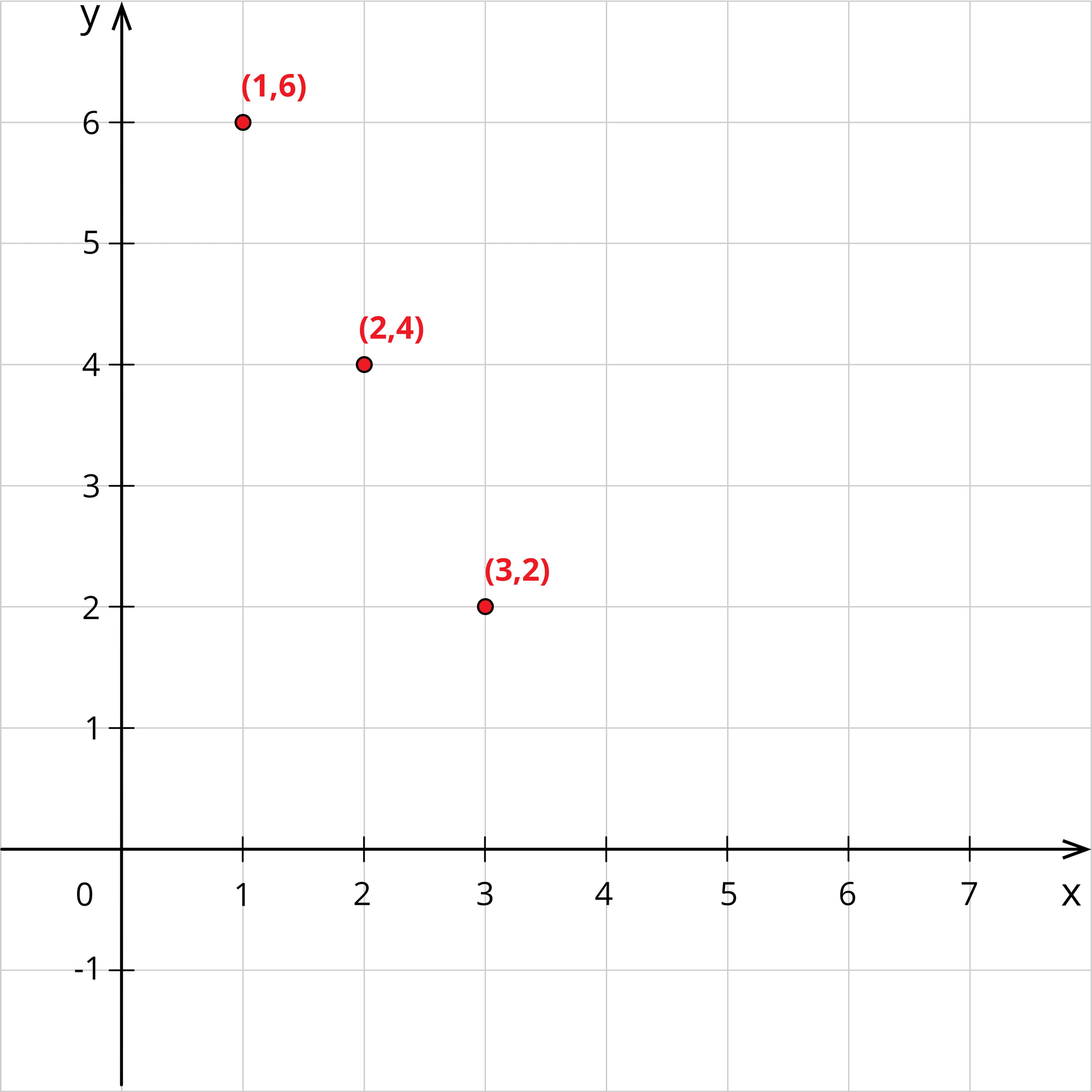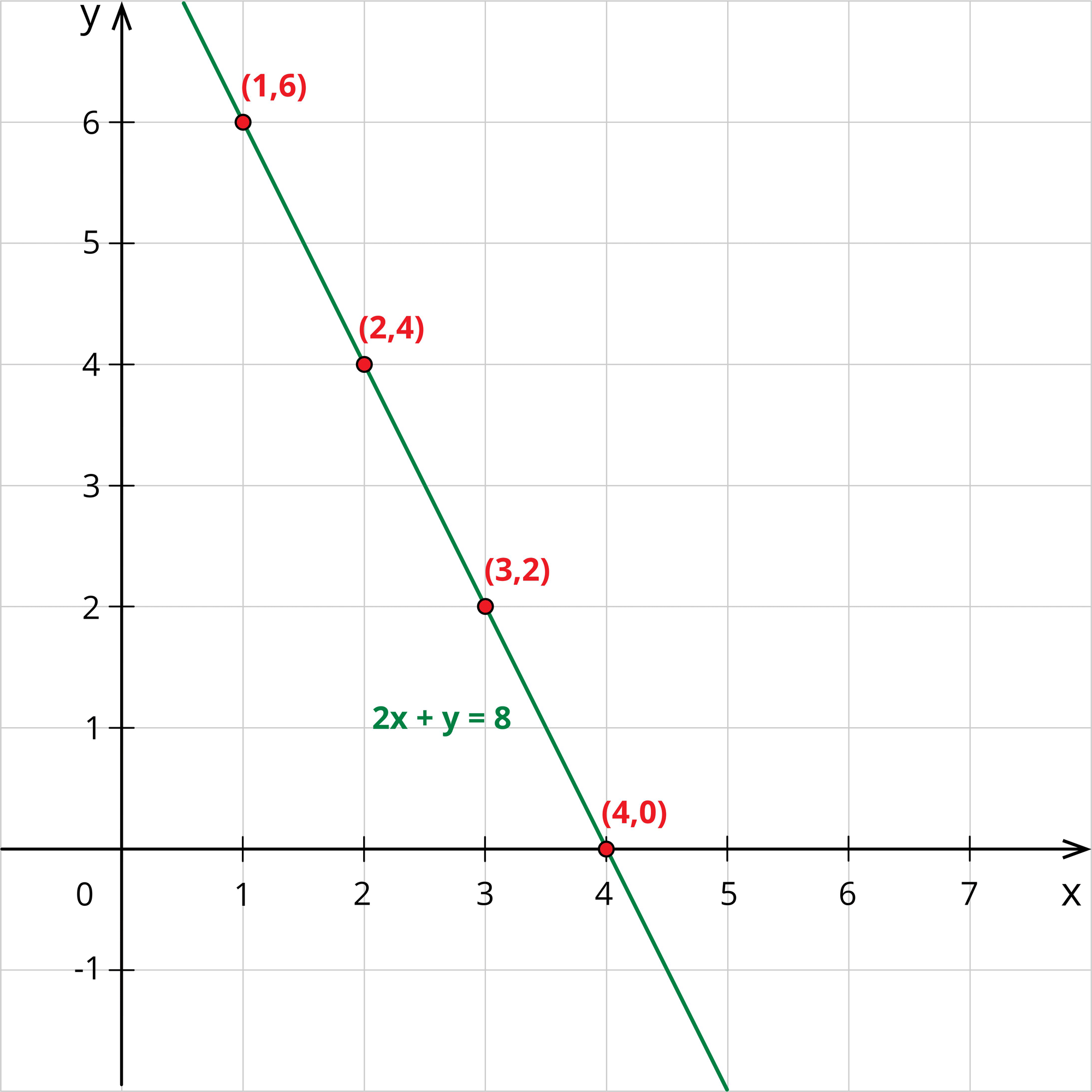
Thus, she gets many number of solutions. Since she is insufficient with the apples and bananas, she again went to the shop and brought \(1\) apple and \(2\) bananas for a total cost of \(₹10\).
Writing in equation, she has:
\(x+2y=10\) ---- \((2)\)
Again, she tries to find each apple and banana's value by substituting the values for \(x\).
When \(x=1\), \(1+2y=10\)\(\Rightarrow 2y=10-1=9\)\(\Rightarrow y=\frac{9}{2}=4.5\)
When \(x=2\), \(2+2y=10\)\(\Rightarrow 2y=10-2=8\)\(\Rightarrow y=\frac{8}{2}=4\)
When \(x=3\), \(3+2y=10\)\(\Rightarrow 2y=10-3=7\)\(\Rightarrow y=\frac{7}{2}=3.5\)
When \(x=4\), \(4+2y=10\)\(\Rightarrow 2y=10-4=6\)\(\Rightarrow y=\frac{6}{2}=3\)
Now, writing these values in the table, we have:
| \(x\) | \(1\) | \(2\) | \(3\) | \(4\) | …. |
| \(y\) | \(4.5\) | \(4\) | \(3.5\) | \(3\) | …. |
Jane plots these points in the graph and draws a line joining these points.
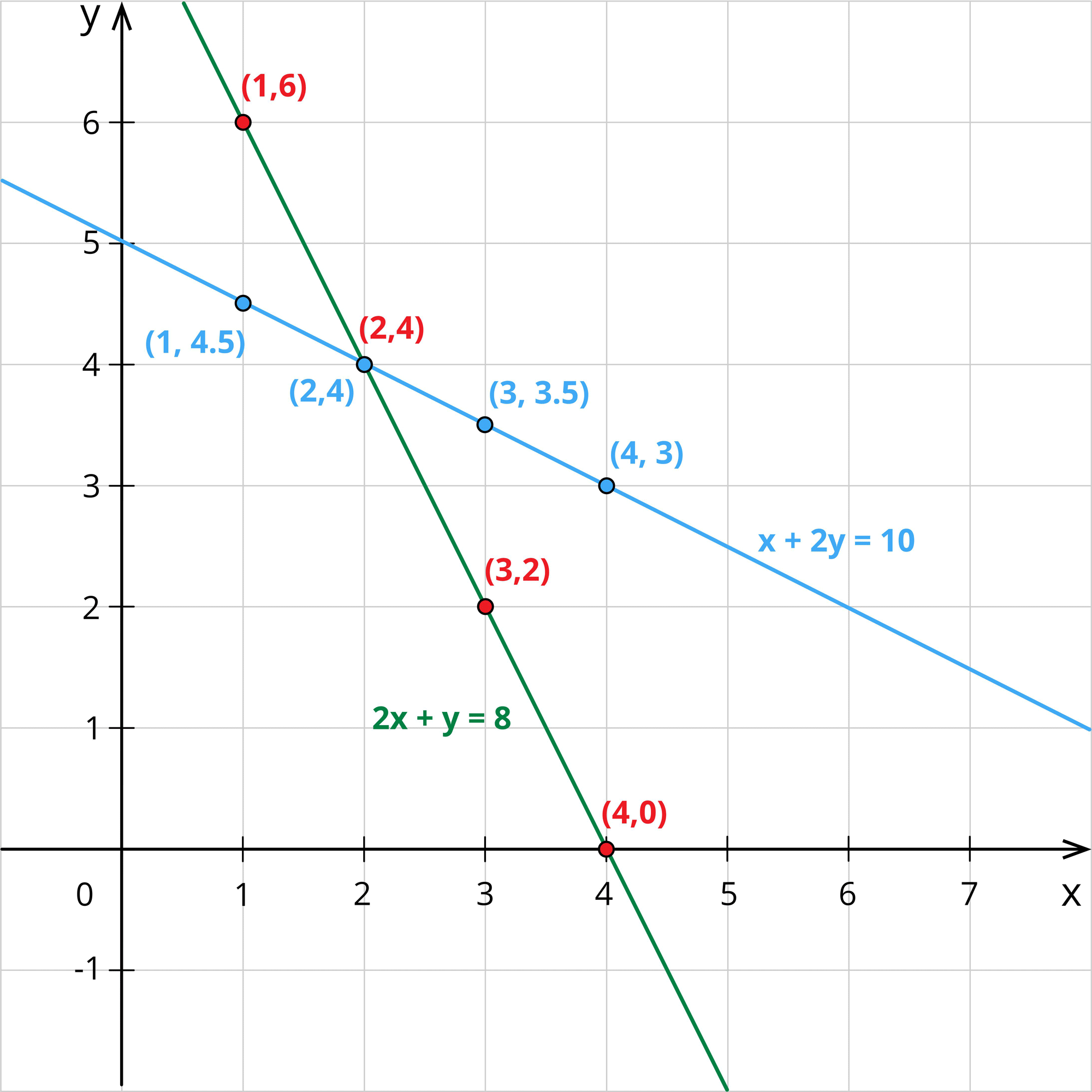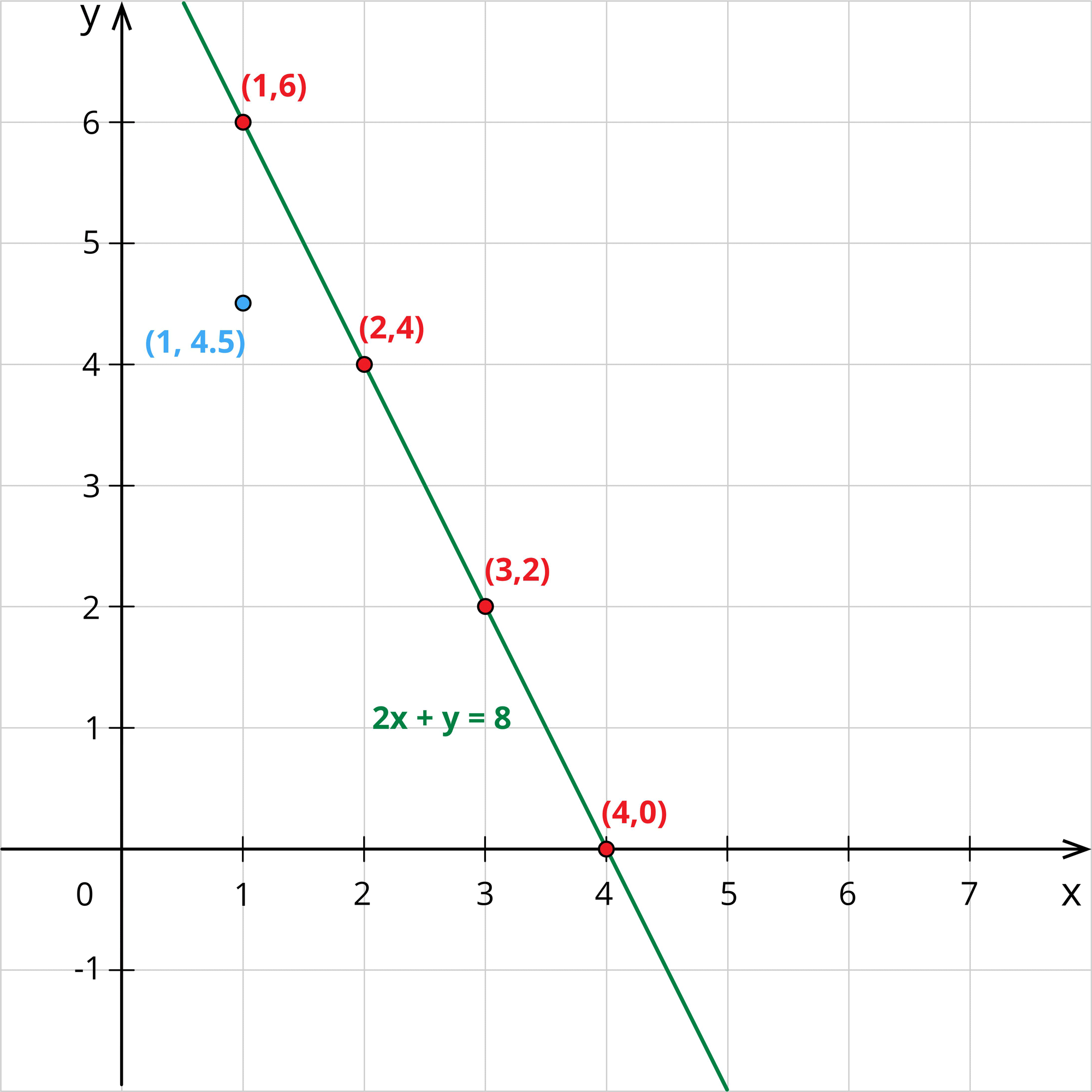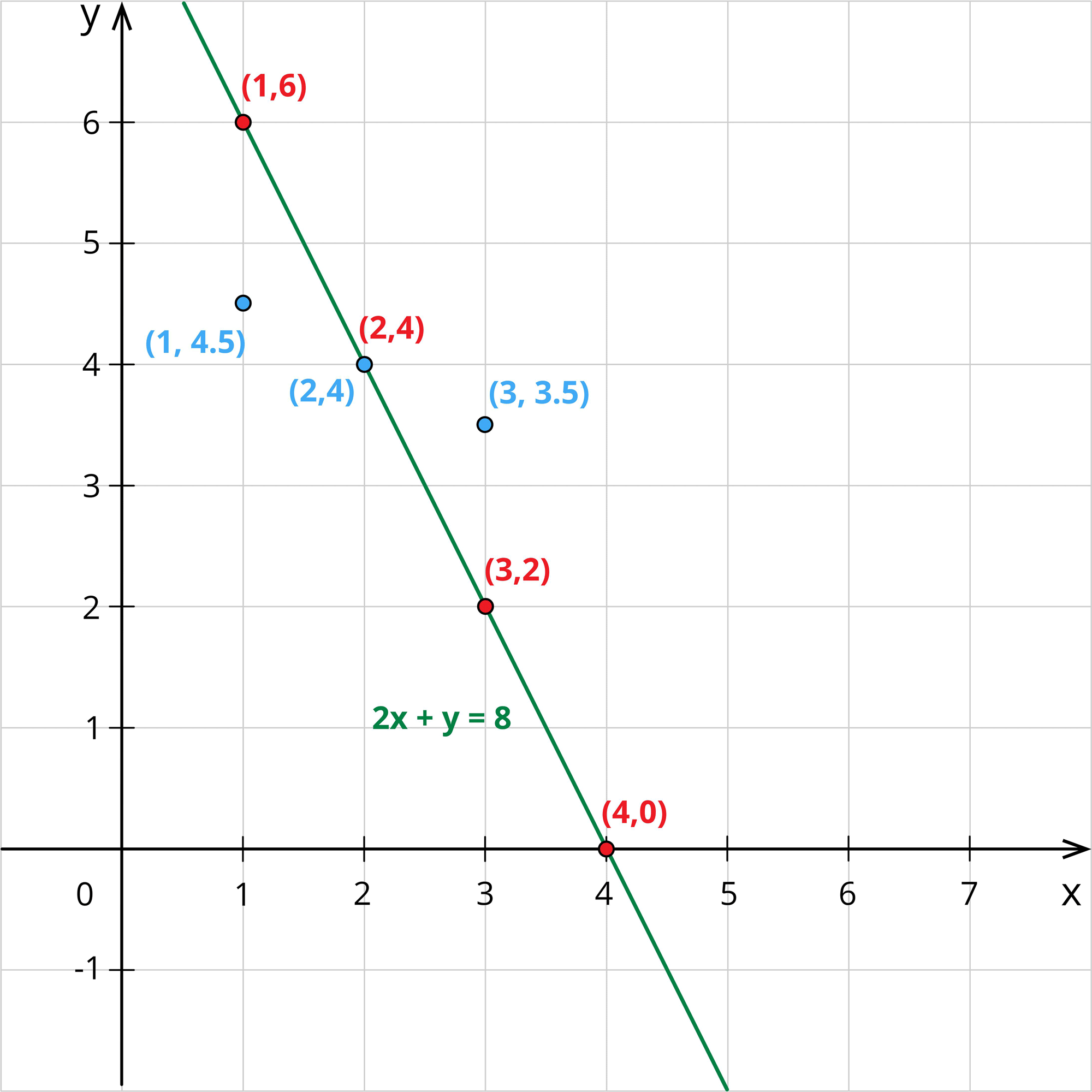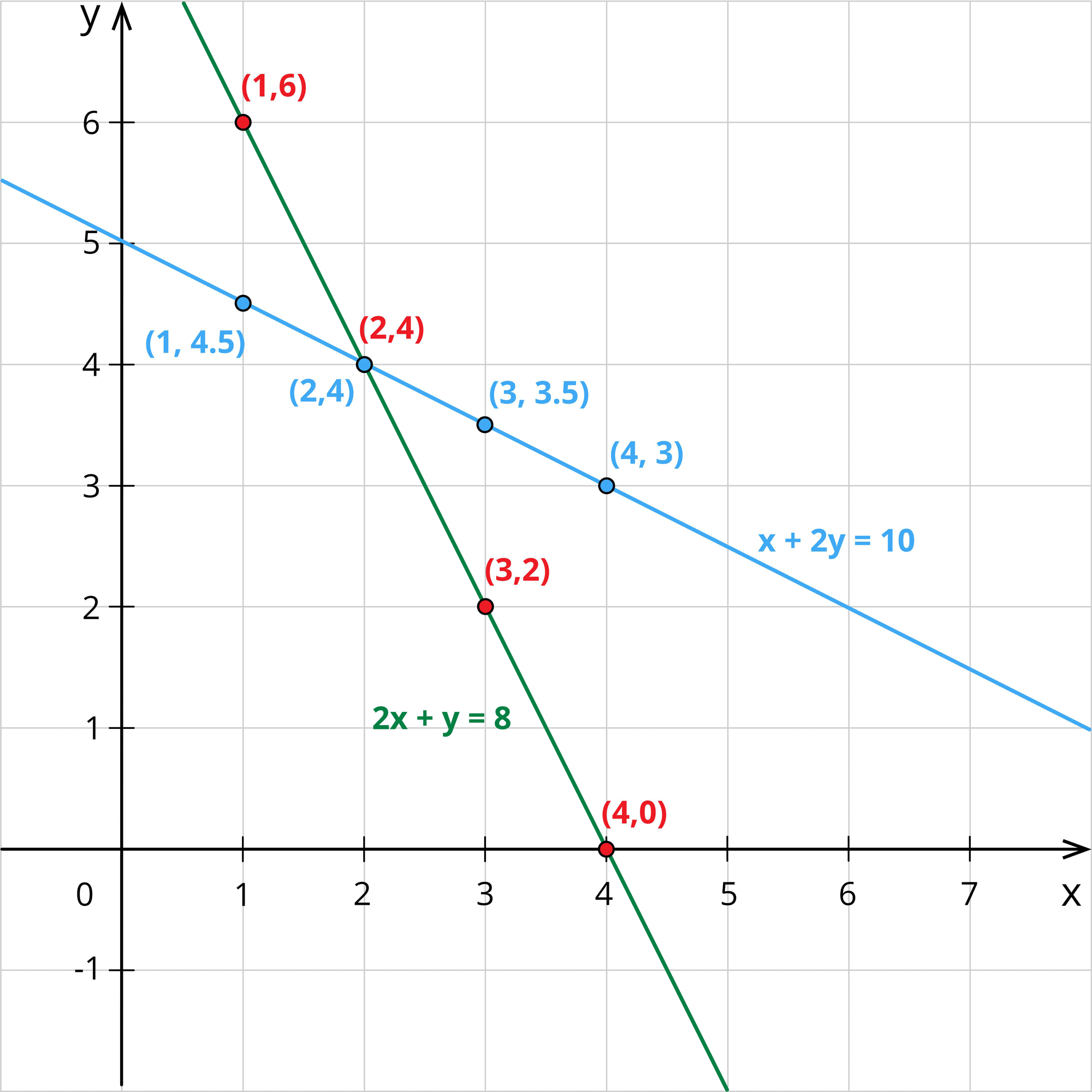
In the graph, she found that the two lines intersect at the point \((2,4)\).
Hence, Jane came to a conclusion that if we solve two equations together, we get an unique solution.
By solving equations \((1)\) and \((2)\), Jane gets the cost of an apple as \($2\) and the cost of a banana as \($4\).
These two equations are called as simultaneous linear equations.
Important!
A solution to the simultaneous linear equation can be found in many ways. They are:
1. Graphical method
2. Substitution method
3. Elimination method
4. Cross multiplication method