Theorem on exterior angles of a cyclic quadrilaterals — lesson. Mathematics State Board, Class 9.

PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

Book Free Demo

Illustration:

Consider a cyclic quadrilateral

$ABCD$ and extend the side

$AB$ to

$E$ .

Here, the angles

$\angle ABC$ and

$\angle CBE$ are a linear pair.

It is known that the sum of the linear angle is

$180^{\circ}$ .

So,

$\angle ABC$

$+$

$\angle CBE$

$=$

$180^{\circ}$

$……$

$\text{equation }(1)$

Also, in a cyclic quadrilateral, the sum of the interior opposite angles is

$180^{\circ}$ .

So,

$\angle ABC$

$+$

$\angle ADC$

$=$

$180^{\circ}$

$……$

$\text{equation }(2)$

From equation

$(1)$ and

$(2)$ , we have:

$\angle ABC$

$+$

$\angle CBE$

$=$

$\angle ABC$

$+$

$\angle ADC$

Hence,

$\angle CBE$

$=$

$\angle ADC$ .

Similarly, all the other angles can be proved.

Based on this result, the following theorem is obtained.

Theorem: If one side of a cyclic quadrilateral is produced, then the exterior angle is equal to the interior opposite angle.

Explanation:

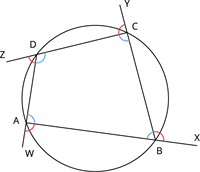
The theorem states that if any side of a cyclic quadrilateral is produced (extended), then the exterior angle formed on that side is the same as the interior opposite angle.

Here, in the figure, the side

$AB$ is produced to

$X$ , the side

$BC$ is produced to

$Y$ , the side

$CD$ is produced to

$Z$ and the side

$DA$ is produced to

$W$ . Then:

$\angle CBX = \angle CDA$

$\angle DCY = \angle DAB$

$\angle ADZ = \angle ABC$

$\angle BAW = \angle BCD$

Example:

Find the unknown angle

$z$ in the figure.

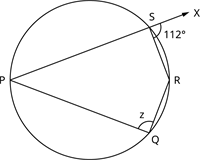
Solution:

By the exterior angle of a cyclic quadrilateral theorem,

$\text{Exterior angle}$

$=$

$\text{Interior opposite angle}$ .

Hence,

$\angle RSX$

$=$

$\angle PQR$

Therefore,

$z$

$=$

$112^{\circ}$ .

Previous theory

Exit to the topic

Next theory

Send feedback

Did you find an error?

Send it to us!

10. Theorem on exterior angles of a cyclic quadrilaterals

Theory: