PDF chapter test TRY NOW
Circle
A Circle is a closed two-dimensional figure with no corners and edges consisting of all the points at an equidistance from a fixed point in a plane.
Parts of a Circle
Centre:
The fixed point in which the circle is described is called the centre of the circle.
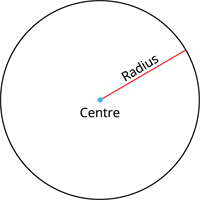
Radius:
The equidistant from the centre to any point on the circle is its radius.
Important!
The line segment joining any point on the circle with its centre is the radius of the circle.
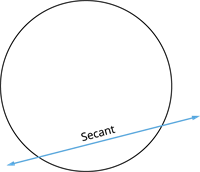
Any line that intersects the circle at two distinct points is called a secant of the circle.
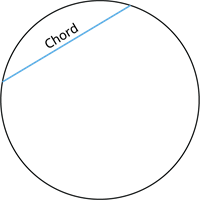
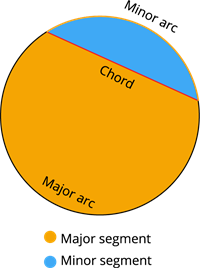
Chord:
The intersecting line having its endpoints on the circle is called a chord of the circle.
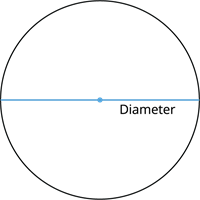
Diameter:
The chord of a circle passing through the centre is called the diameter of the circle.
Important!
Properties of the diameter:
- It is the line segment that bisects the circle.
- It is the largest chord in the circle.
- It is the line of symmetry for the circle.
- It is twice the length of the radius.
Circumference:
The boundary line of the circle is called its circumference.
Arc:
Any portion of the circumference of a circle is called an arc. It is denoted using the symbol "".
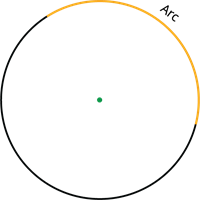
Here, the shorter arc(yellow) is called the minor arc and the longer arc(black) is called the major arc.
Segment:
The region enclosed by the chord and the arc is called the segment of the circle.

Important!
The region enclosed by the chord and the minor arc is called the minor segment, and the region enclosed by the chord and the major arc is called the major segment.
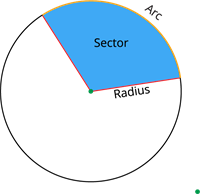
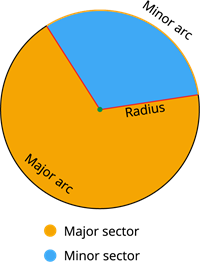
Sector:
The region enclosed between two radii and the arc is called the sector.
Important!
The region enclosed by the two radii and the minor arc is called the minor sector, and the region enclosed by the two radii and the major arc is called the major sector.
Concentric circles
The circles with a common centre and with different radii are called concentric circles.
Example:
Water ripples caused by a drop of water.

Congruent circles
Two or more circles having the same radii are said to be congruent.
Example:
The wheels of a cycle are identical in shape and size.

Important!
If two arcs of a circle subtend the same angle at the centre, then the arcs are congruent.
Position of a point with respect to a circle
Consider any point on the circle in a plane, then:
- If the distance between the centre and the point is equal to the radius of the circle, then the point lies on the circle.
- If the distance between the centre and the point is less than the radius of the circle, then the point lies inside the circle.
- If the distance between the centre and the point is greater than the radius of the circle, then the point lies outside the circle.
Therefore, the circle divides the plane into three distinct region in which it lies.
Important!
The centre of the circle always lie in the interior of the circle.
Reference:
https://pixy.org/5939397/
https://pixy.org/4801720/
