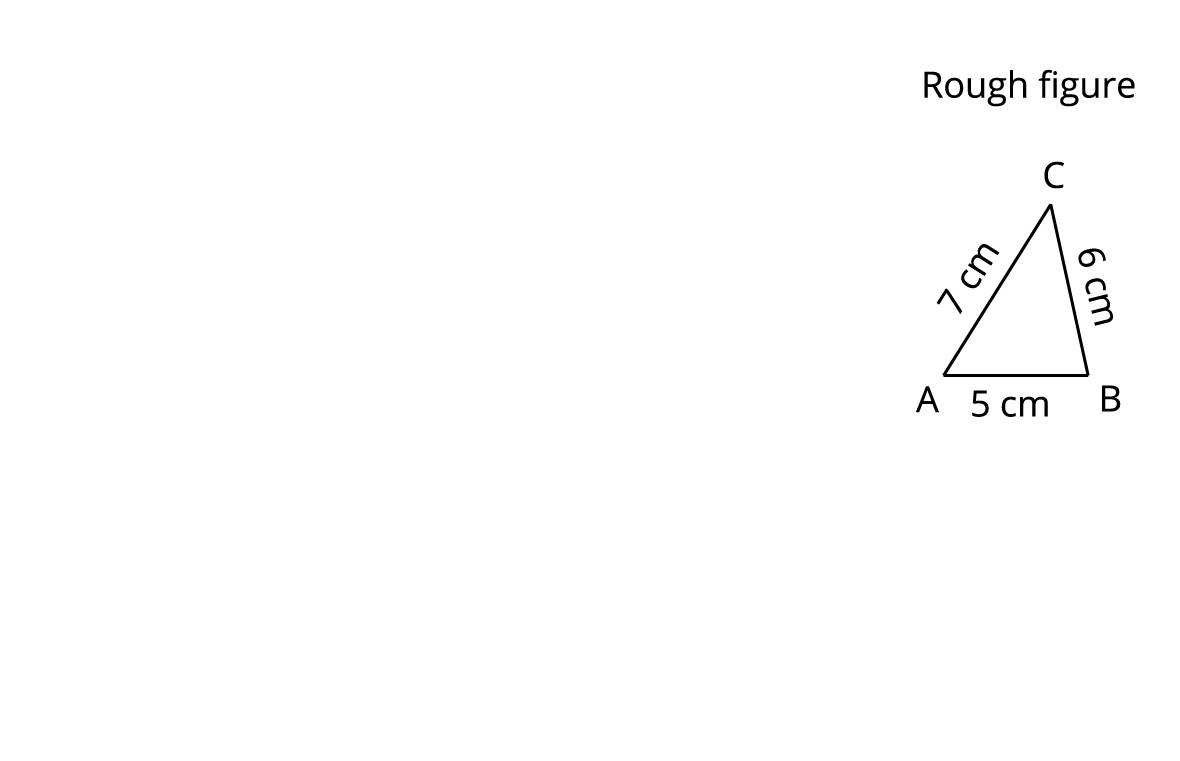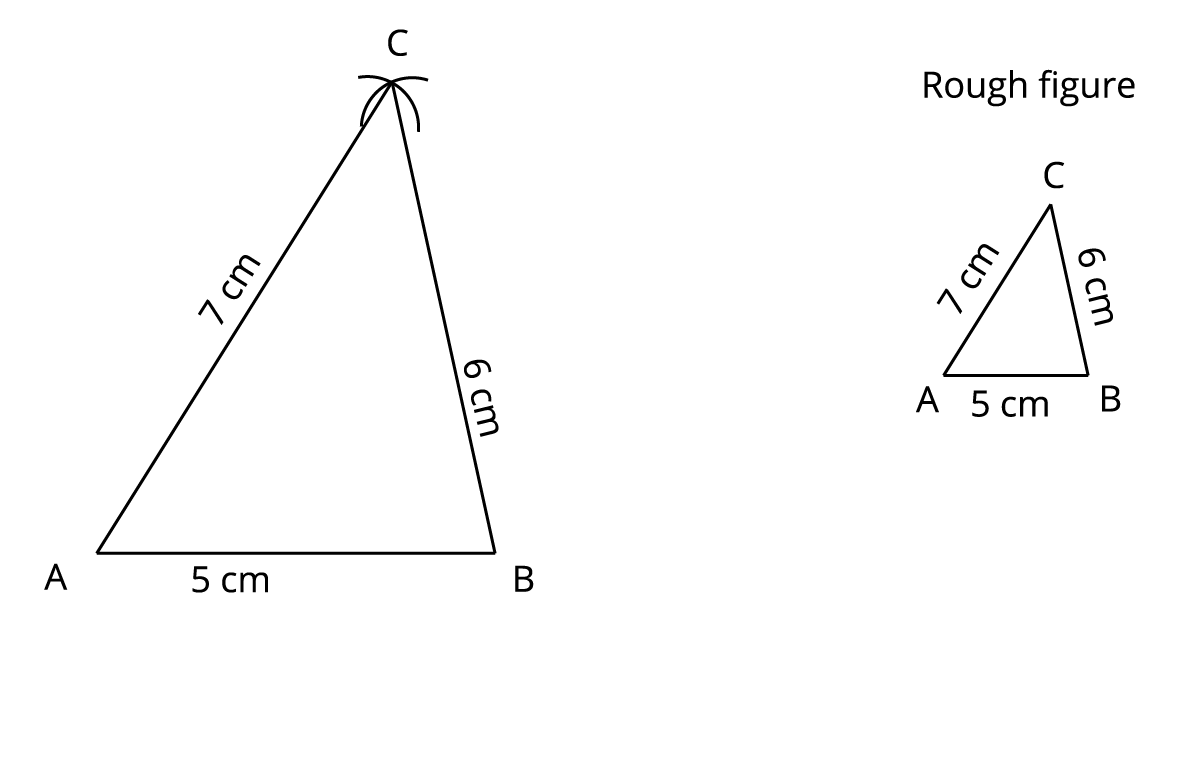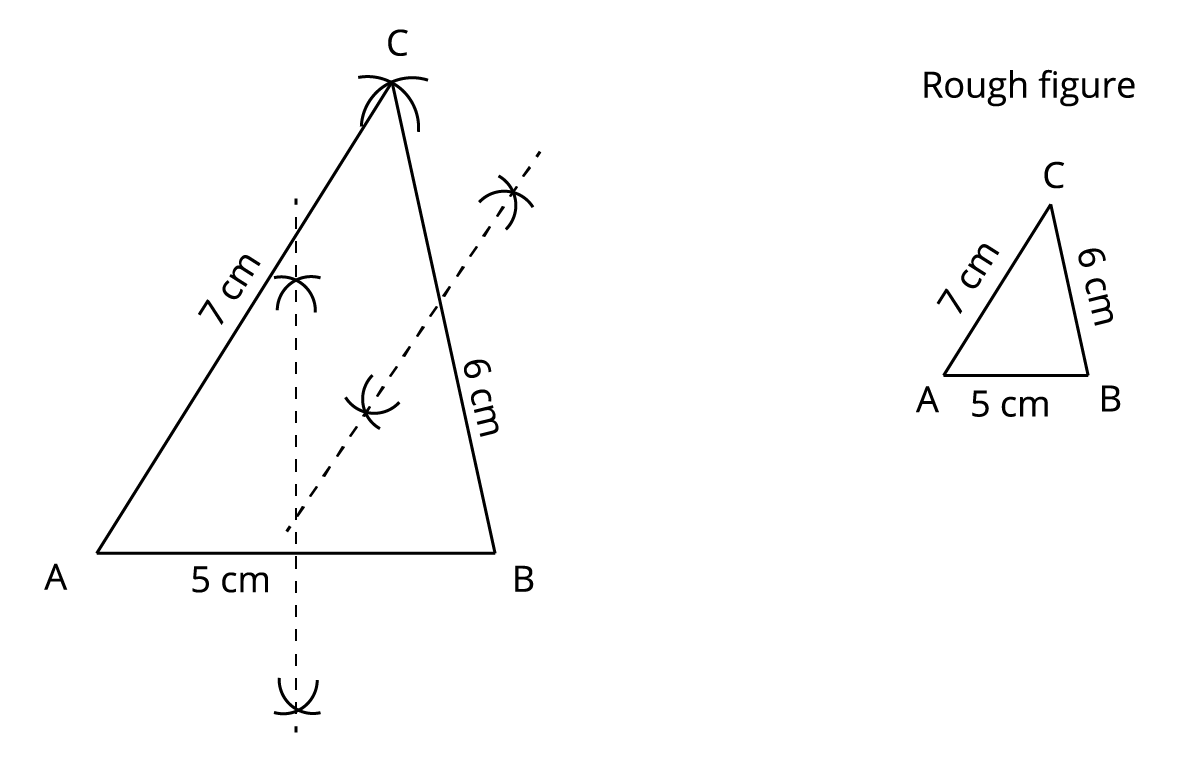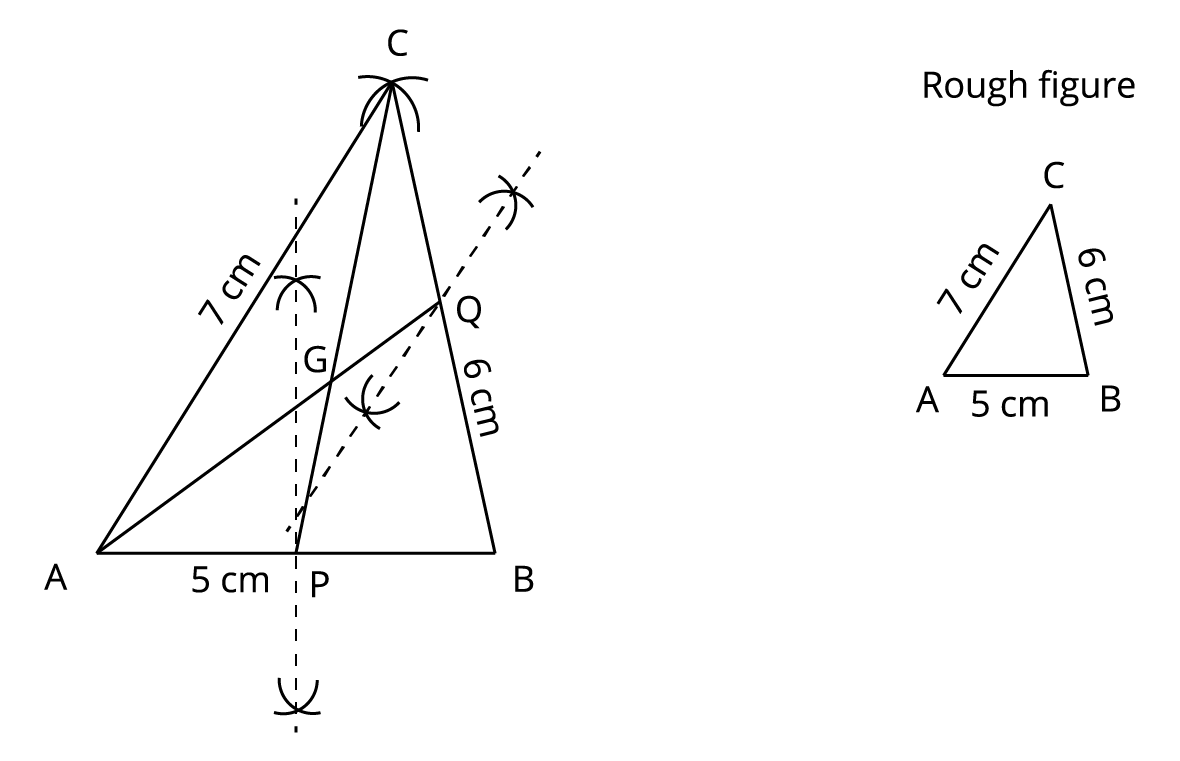UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreCentroid: It is the point of concurrency of a triangle formed by the intersection of its medians. It is denoted by \(G\).
Working rule to construct the Centroid of a Triangle
Case 1:
Given the length of two sides of a triangle and the measure of one of its interior angle.
Example:
Construct a triangle \(ABC\) given \(AB = 8\) \(cm\), \(BC = 6\) \(cm\) and \(\angle BAC = 55^{\circ}\) and locate its centroid.
Construction:
Step 1: Draw a rough figure for the given question to get the picture of the triangle that is to be constructed.
Step 2: Draw a line segment \(AB = 8\) \(cm\) using the ruler.
Step 3: With \(A\) as centre, mark an angle \(55^{\circ}\) using the protractor and name it as \(X\). Now join \(AX\).
Step 4: With \(B\) as centre, measure \(6\) \(cm\) in the compass and cut an arc intersecting \(AX\) and mark it as \(C\).
Step 5: Draw the perpendicular bisectors of any two sides of the triangle \(AB\) and \(BC\) (say) to find the mid-points of the sides, respectively.
Step 6: Mark the intersecting point of the perpendicular bisectors and the sides \(AB\) and \(BC\) as \(P\) and \(Q\) respectively.
Step 7: Draw the medians \(AQ\) and \(CP\) to meet each other at \(G\), which is the centroid of the triangle.
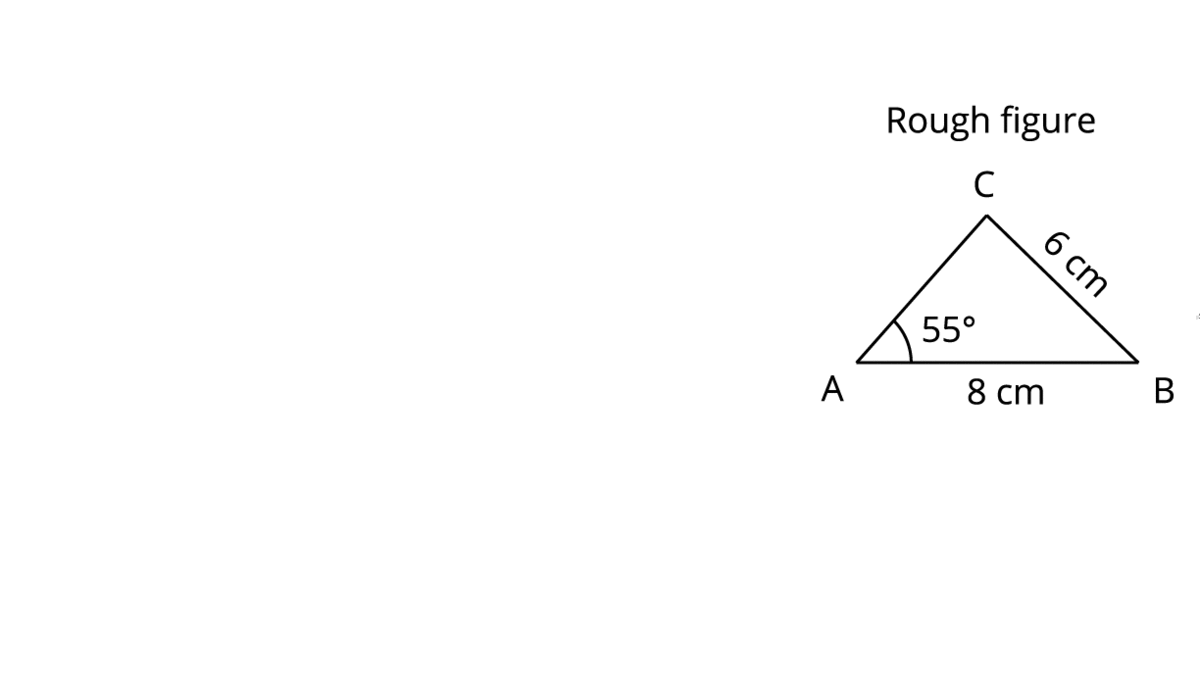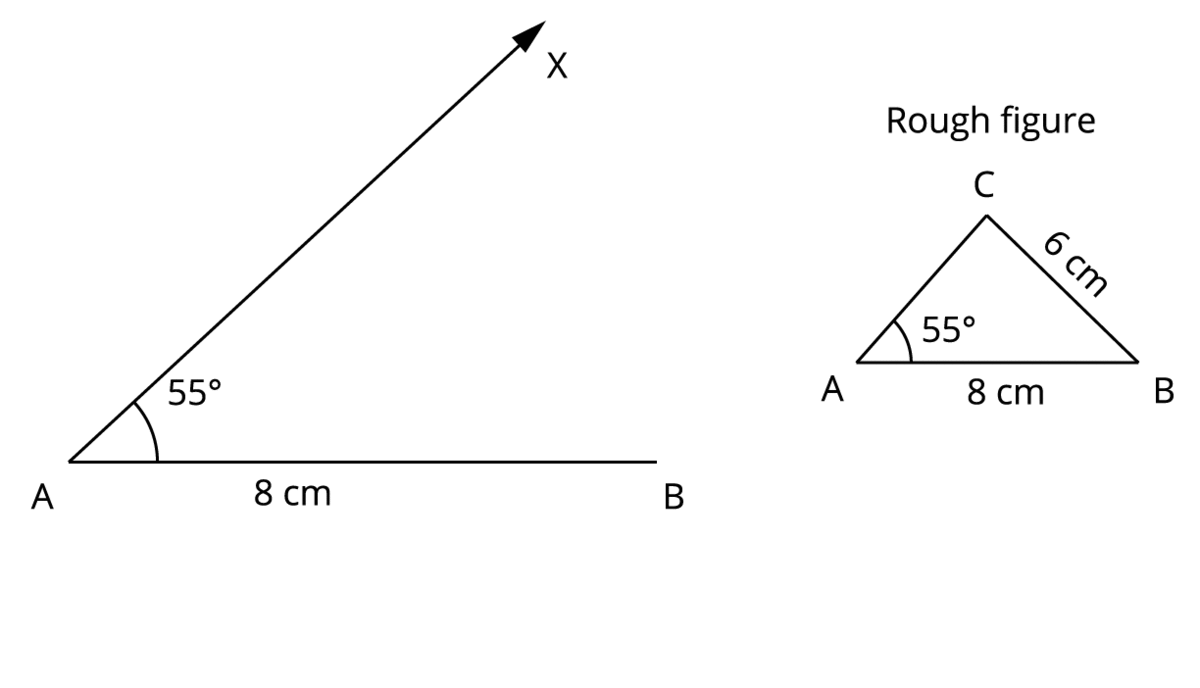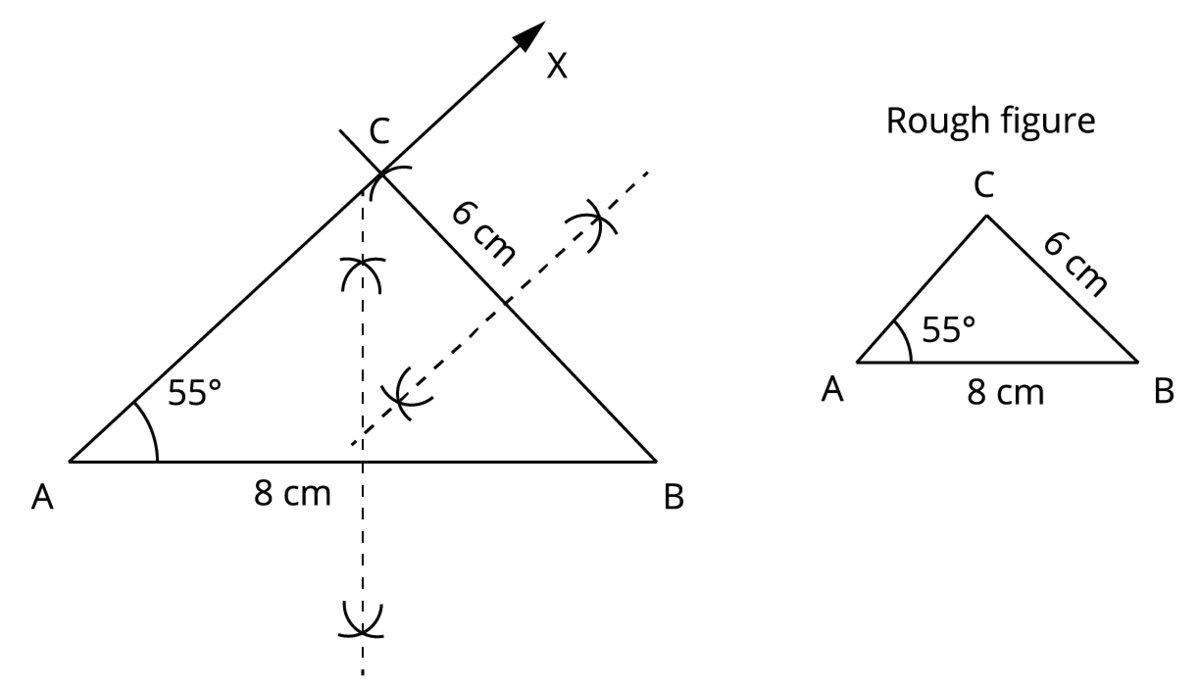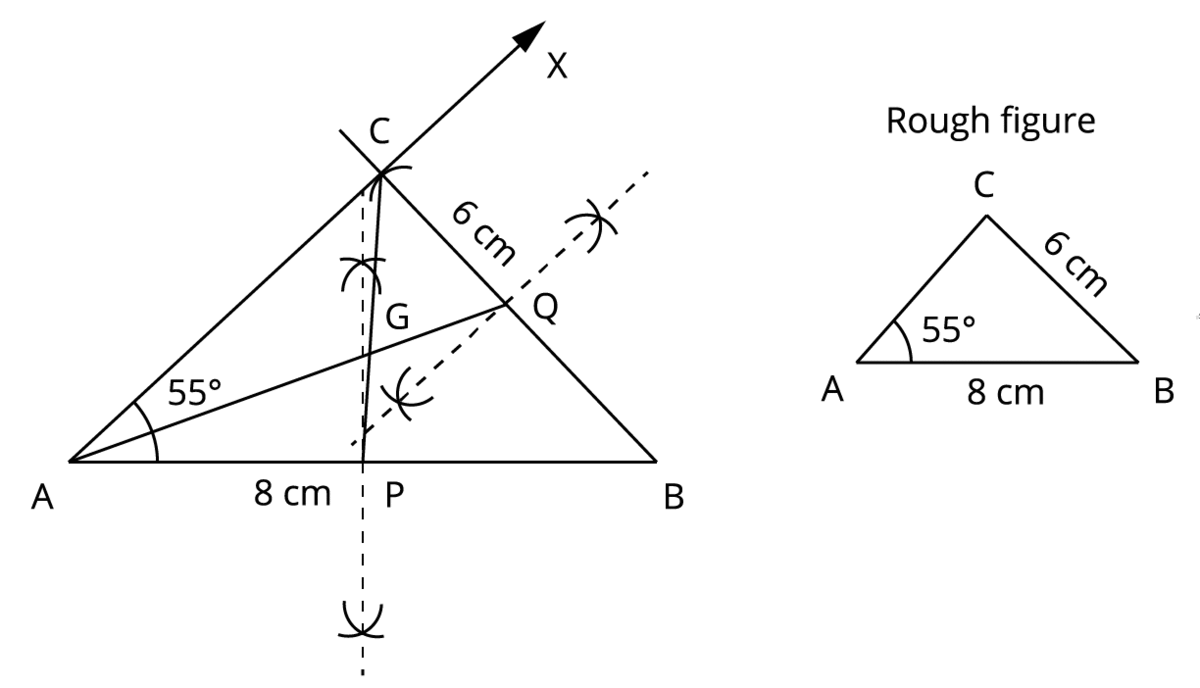
Case 2:
Given the length of all the three sides of a triangle.
Example:
Construct a triangle \(ABC\) given \(AB = 5\) \(cm\), \(BC = 6\) \(cm\) and \(CA = 7\) \(cm\) and locate its centroid.
Construction:
Step 1: Draw a rough figure for the given question to get the picture of the triangle that is to be constructed.
Step 2: Draw a line segment \(AB = 5\) \(cm\) using the ruler.
Step 3: With \(B\) and \(A\) as centre, cut arcs of radius \(6\) \(cm\) and \(7\) \(cm\) respectively to meet each other at \(C\).
Step 4: Draw the perpendicular bisectors of any two sides of the triangle \(AB\) and \(BC\) (say) to find the mid-points of the sides, respectively.
Step 5: Mark the intersecting point of the perpendicular bisectors and the sides \(AB\) and \(BC\) as \(P\) and \(Q\), respectively.
Step 6: Draw the medians \(AQ\) and \(CP\) to meet each other at \(G\), which is the centroid of the triangle.
Register for free to see more content